Test: Co-ordinate Geometry- 3 - GMAT MCQ
15 Questions MCQ Test - Test: Co-ordinate Geometry- 3
For any triangle T in the xy–coordinate plan, the center of T is defined to be the point whose x–coordinate is the average (arithmetic mean) of the x–coordinates of the vertices of T and whose y–coordinate is the average of the y–coordinates of the vertices of T. If a certain triangle has vertices at the points (0,0) and (6,0) and center at the point (3,2), what are the coordinates of the remaining vertex?
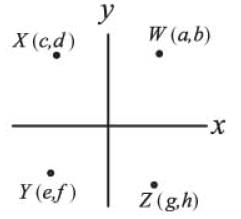
In the rectangular coordinate plane points X and Z lie on the same line through the origin and points W and Y lie on the same line through the origin. If a2 + b2 = c2 + d2 and e2 + f2 = g2 + h2, what is the value of length XZ – length WY?

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In the xy-coordinate system, what is the slope of the line that goes through the origin and is equidistant from the two points P = (1, 11) and Q = (7, 7)?
What is the slope of the line represented by the equation x + 2y = 1?
A certain square is to be drawn on a coordinate plane. One of the vertices must be on the origin, and the square is to have an area of 100. If all coordinates of the vertices must be integers, how many different ways can this square be drawn?
Line L contains the points (2,3) and (p,q). If q = 2, which of the following could be the equation of line m, which is perpendicular to line L?
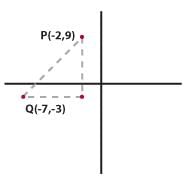
The (x, y) coordinates of points P and Q are (-2, 9) and (-7, -3), respectively. The height of equilateral
triangle XYZ is the same as the length of line segment PQ. What is the area of triangle XYZ?
The line 3x + 4y = 8 passes through all of the quadrants in the coordinate plane except:
The coordinates of points A and C are (0, -3) and (3, 3), respectively. If point B lies on line AC between points A and C, and if AB = 2BC, which of the following represents the coordinates of point B?
In the xy-coordinate system, rectangle ABCD is inscribed within a circle having the equation x2 + y2 = 25. Line segment AC is a diagonal of the rectangle and lies on the x-axis. Vertex B lies in quadrant II and vertex D lies in quadrant IV. If side BC lies on line y = 3x + 15, what is the area of rectangle ABCD?
The line represented by the equation y = 4 – 2x is the perpendicular bisector of line segment RP. If R has the coordinates (4, 1), what are the coordinates of point P?
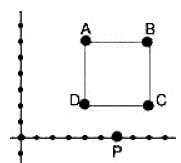
A certain computer program randomly generates equations of lines in the form y = mx + b. If point P
is a point on a line generated by this program, what is the probability that the line does NOT pass through figure ABCD?
In the rectangular coordinate system, a line passes through the points (0,5) and (7,0). Which of the following points must the line also pass through?
Which of the following equations represents a line that is perpendicular to the line described by the equation 3x + 4y = 8?
How many units long is the straight line segment that connects the points (-1,1) and (2,6) on a rectangular coordinate plane?


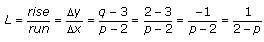
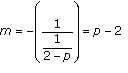
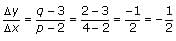
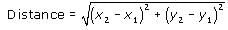
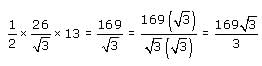
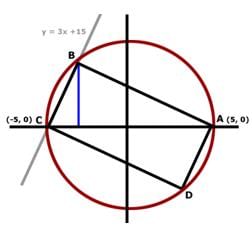
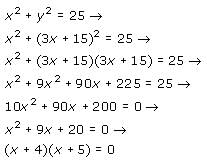 So the two possible values of x are -4 and -5. Therefore, the two points where the circle and line intersect (points B and C) have x-coordinates -4 and -5, respectively. Since the x-coordinate of point C is -5 (it has coordinates (-5, 0)), the x-coordinate of point B must be -4. We can plug this into the equation and solve for the y-coordinate of point B:
So the two possible values of x are -4 and -5. Therefore, the two points where the circle and line intersect (points B and C) have x-coordinates -4 and -5, respectively. Since the x-coordinate of point C is -5 (it has coordinates (-5, 0)), the x-coordinate of point B must be -4. We can plug this into the equation and solve for the y-coordinate of point B: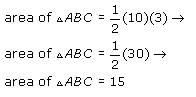
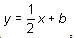 where b represents the unknown y-intercept.
where b represents the unknown y-intercept.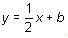 we can plug 4 in for x and 1 in for y as follows:
we can plug 4 in for x and 1 in for y as follows: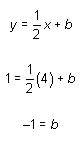
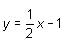

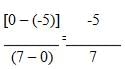
 which means that m (the slope)
which means that m (the slope) 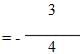 . The slope of a line perpendicular to this line must be 4/3, the negative reciprocal of -3/4.
. The slope of a line perpendicular to this line must be 4/3, the negative reciprocal of -3/4.