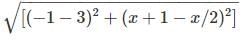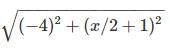Test: Numeric Entry- 1 - GRE MCQ
15 Questions MCQ Test Section-wise Tests for GRE - Test: Numeric Entry- 1
The denominator of a fraction is 4 less than the numerator. If the denominator is decreased by 2 and the numerator is increased by 1, then the numerator is eight times the denominator. Find the numerator of the fraction.
A father is four times as old as his son is. Five years back he was seven times as old as his son was then. What is the present age of the father?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the positive value of x, for which AB = 5 units for points A(3,x/2) and B(-1,x+1).
Find the mid-point of the line joining the points P(3, - 1, 2) and Q(3, 3, - 2)?
When two lines are parallel, what is the difference of their slopes equal to?
For what value of k is the line (k-3)x-(4-k2)y+k2-7k+6=0 parallel to the x axis? [k2=k*k]
The sum of three numbers is 132. The first number is twice the second and the third number is one-third of the first. Find the first number
Three-fourth of a number is 150 greater than three-fourteenth of the number. Find the number.
If a/(a+b) = 17/23, then fill in the blank (a+b)/(a-b) = -------/11
5 men can complete a work in 2 days, 4 women can complete it in 3 days and 5 children can complete it in 3 days. In how many days can 1 man, 1 woman and 1 child complete it working together?
In a kilometer race A can give B a start of 50 meters and B can give C a start of 40 meters. A start of how many meters can A give C in a 2 km race?
On what sum is the difference in compound interest and simple interest for 3 years at 5% per annum Rs.61?
|
30 tests
|