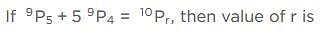Test: Numeric Entry- 5 - GRE MCQ
15 Questions MCQ Test Section-wise Tests for GRE - Test: Numeric Entry- 5
The average of 6 observations is 12. When the seventh observation is added the average decreases by 1. Find the seventh observation.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Pam bought some apples for Rs.110. Had the shopkeeper given him one extra apple, each apple would have cost him Re.1 lesser. How many apples did he buy?
Find the length of the longest stick that can be filled in a cuboid of length 12 cm, breadth 5 cm and height 84 cm.
The length of the square is increased by 30%. The breadth of the square is increased by 20%. By what percent does the area of the rectangle exceed the area of the square?
The sum of the squares of the numbers is 37/6 times their product. The sum of the numbers is 35. Find the difference of the two numbers.
The item was listed at Rs 65 and sold at Rs. 56.16. Two successive discounts were given on the item and the first discount was 10%. Find the second discount percent.
A man rows 12 km upsteram and 22 km downstream. He takes 5 hours to complete each part of his journey. What is the speed of the water in the stream?
Two numbers are in ratio 6:13. The least common multiple of the two numbers is 312. Find the sum of the two numbers.
ABC is an isosceles triangle with AC=CB. A square whose one side is the altitude of the triangle from the vertex to the non-equal side has perimeter 140 cm. The area of the triangle is equal to 420 sq.cm. Find the length of the equal sides of the triangle.
The lengths of the two diagonals of a rhombus are 72 cm and 30 cm. Find the length of each side.
In a groups of hens and cows, the number of heads is 48 and the number of feet is 140. How many cows are there in the group?
|
30 tests
|