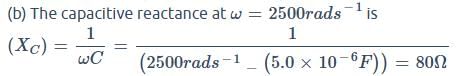Test: Alternating Current - NEET MCQ
30 Questions MCQ Test Physics Class 12 - Test: Alternating Current
For a series LCR circuit the input impedance at resonance
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A resistor of 100 Ω and a capacitor of 10μF are connected in series to a 220 V 50 Hz ac source. Voltage across the capacitance and resistor are
The current amplitude in a pure inductor in a radio receiver is to be 250 μA when the voltage amplitude is 3.60 V at a frequency of 1.60 MHz (at the upper end of the AM broadcast band). If the voltage amplitude is kept constant, what will be the current amplitude through this inductor at 16.0 MHz?
A 0.180-H inductor is connected in series with a 90.0 Ω resistor and an ac source. The voltage across the inductor is (-12.0 V)sin(480 rad/s)t What is VR at t = 2ms ?
The main reason for preferring usage of AC voltage over DC voltage
A sinusoidal voltage of peak value 283 V and frequency 50 Hz is applied to a series LCR circuit in which R = 3 Ω, L = 25.48 mH, and C = 796 μF. Power dissipated in the circuit; and the power factor are
A 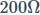 resistor is connected in series with a
resistor is connected in series with a 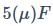 capacitor. The voltage across the resistor is vR = (1.20 V) cos(2500 rad/s)t . Capacitive reactance is
capacitor. The voltage across the resistor is vR = (1.20 V) cos(2500 rad/s)t . Capacitive reactance is
In the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the inductor.
In a series RLC circuit R = 300 Ω , L = 60 mH, C = 0.50 μF applied voltage V= 50 V and ω = 10,000 rad/s. voltages VR,VL and VC are
In an L-R-C series circuit, the rms voltage across the resistor is 30.0 V, across the capacitor it is 90.0 V, and across the inductor it is 50.0 V. Rms voltage of the source is
A radio can tune over the frequency range of a portion of MW broadcast band: (800 kHz to 1200 kHz). If its LC circuit has an effective inductance of 200 μH, what must be the range of its variable capacitor?
Average power supplied to an inductor over one complete cycle
A light bulb is rated at 50W for a 220 V supply. The resistance of the bulb, the peak voltage of the source and the rms current through the bulb are
An electric hair dryer is rated at 1500 W (the average power) at 120 V (the rms voltage). Calculate (a) the resistance, (b) the rms current, and (c) the maximum instantaneous power. Assume that the dryer is a pure resistor.
You have a 200.0 ΩΩ resistor, a 0.400-H inductor, a 5.0 μF capacitor, and a variable frequency ac source with an amplitude of 3.00 V. You connect all four elements together to form a series circuit. Frequency at which current in the circuit is greatest and its amplitude are
An LC circuit contains a 20 mH inductor and a 50 μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Natural frequency of the circuit is
A hair dryer meant for 110V 60Hz is to be used in India . If 220 V is the supply voltage in India , the turns ratio for a transformer would be
You have a 200.0 ΩΩ resistor, a 0.400-H inductor, 5.0 μF a capacitor, and a variable frequency ac source with an amplitude of 3.00 V. You connect all four elements together to form a series circuit. Current amplitude at an angular frequency of 400 rad/s is
A lamp is connected in series with a capacitor and connected to an AC source. As the capacitance value is decreased.
A 100 μF capacitor in series with a 40 Ω resistance is connected to a 110 V, 60 Hz supply. Maximum current in the circuit and time lag between the current maximum and the voltage maximum are
You have a special light bulb with a very delicate wire filament. The wire will break if the current in it ever exceeds 1.50 A, even for an instant. What is the largest root-mean-square current you can run through this bulb?
Average power supplied to a capacitor over one complete cycle
|
97 videos|336 docs|104 tests
|