Test: Biot Savart Law - NEET MCQ
10 Questions MCQ Test Physics Class 12 - Test: Biot Savart Law
If we double the radius of a current carrying coil keeping the current unchanged. what happens to the magnetic field at its Centre?
A circular arc of metallic wire subtends an angle π/2 at center. If it carries current I and its radius of curvature is r, then the magnetic field at the center of the arc is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The magnetic field B on the axis of a circular coil at distance x far away from its centre are related as:
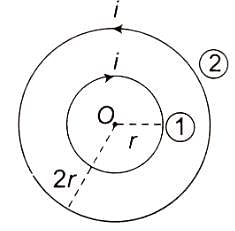
Two concentric coils carry the same current in opposite directions. The diameter of the inner coil is half that of the outer coil. If the magnetic field produced by the outer coil at the common centre are 1 T, the net field at the centre is
The magnetic field due to current element depends upon which of the following factors:
A circular coil of radius r carries current I. The magnetic field at its center is B. at what distance from the center on the axis of the coil magnetic field will be B/8
A circular loop of radius 0.0157 m carries a current of 2 A. The magnetic field at the centre of the loop is
A straight conductor carrying current I is split into circular loop as shown in figure a , the magnetic induction at the center of the circular loop is
The magnetic field due to circular coil of 200 turns of diameter 0.1m carrying a current of 5A at a point on the axis of the coil at a distance 0.15m from the center of the coil will be
Wire of length l, carries a steady current I. It is bent first to form a circular coil of one turn. The same wire of same length is now bent more sharply to give two loops of smaller radius the magnetic field at the centre caused by the same current is
|
97 videos|336 docs|104 tests
|