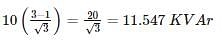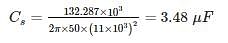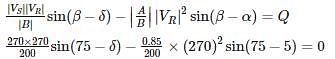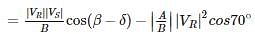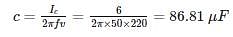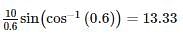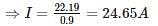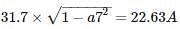Test: Power Systems- 4
10 Questions MCQ Test GATE Electrical Engineering (EE) 2023 Mock Test Series | Test: Power Systems- 4
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the following statements:
The VAR injection in a power system is obtained by:
1. Tap changing transformers
2. Synchronous condensers
3. Capacitor and inductor banks
4. Inductor banks
Which of the following statements given above are correct?
The purpose of a tap changer is to regulate the output voltage of a transformer. It does this by altering the number of turns in one winding and thereby changing the turn’s ratio of the transformer.
Synchronous condensers and capacitor banks are used to inject leading VAR into system where as inductor banks are used to inject lagging VAR into system.
An induction motor operating at 0.8 pf lag consuming 500 kW. A zero real power consuming synchronous motors is connected across the induction motor raise the power factor to unity. The reactive power drawn by synchronous motor is___ (kVAR)
P = 500 kW, Power factor = 0.8
KVA = 500/0.8 = 625 KVA
Reactive power drawn = 625 × 0.6 = 375 kVAR
To rise the power factor to unity, the total kVAR drawn by induction motor should be supplied by synchronous motor. KVAR drawn by synchronous motor is 375 kVAR.
A 10 kW induction motor initially operating on a power factor of 0.5 lagging. If power factor is improved to 0.866 lagging than what is the value of kVAr raised
Raised KV Ar = 10(tan600 − tan300) = 
Shunt capacitor are used to raise the power factor of the load of 150 kW from 0.75 lag to unity, the supply being 3 – phase at 11 kV. In star bank the capacitance will be – (in μF)
KV AR = P tan ϕ
= 150 × 103 × 0.88 = 132.287 × 103
At an Industrial substation with a 4 MW load a capacitor of 2.5 MVAR is installed to maintain the load power factor at 0.97 lag. If the capacitor goes out of service, the load power factor becomes –
PL = 4MW
QC = 2.5MV AR
Pf = 0.97 lag
⇒ Power factor =cosϕ=0.75lag
A 270 KV transmission line has the following line constants A = 0.85∠5° ; B = 200∠75°. What is the power that can be received if the voltage profile at each end is maintained at 270 KV (in MW) –
Given |VS|= |VR| = 270 KV, α = 5°, β = 75°
since the power is received at unity power factor QR = 0
⇒ δ = 22°
Power received PR
= 219.6 – 105.96 = 113.64 MW
A single phase 50 Hz motor takes 20 A at 0.75 power factor lagging from a 220 V sinusoidal supply. The capacitance required to be connected in parallel to raise the power factor to 0.9 lagging is ______ (in μF)
I1 = 20A, f = 50 Hz
cosϕ1 = 0.75 ⇒ ϕ1 = 41.41∘ ⇒ tanϕ1 = 0.88
cosϕ2 = 0.9 ⇒ ϕ2 = 25.84∘ ⇒ tanϕ2 = 0.48
Ic = I1 cosϕ1 (tanϕ1 − tanϕ2)
= (20) (0.75) (0.88 – 0.48) = 6 A
A single – phase inductive load is drawing 10 MW at 0.6 power factor lagging. A capacitor is added in parallel across the load to improve the power factor to 0.85. What is the reactive power required for the capacitor?
Initially when the real power is 10 MW and power factor is 0.6, the reactive power is 
Now when the capacitor is added, improved power factor is
cos-1 0.85 = 31.79°
Reactive power is 10 tan 31.79° = 6.2 VAR
Reactive power needed for the capacitor
= Qc = - (13.33 – 6.2)
= - 7.13 MVAR
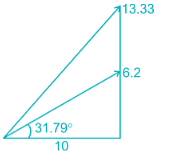
A single phase motor connected to 400V, 50Hz supply takes 31.7 A at a power factor of 0.7 lagging. Calculate the capacitance (in μF) required in parallel with the motor to raise the power factor to 0.9 lagging.
Active component of IM = IM cosϕM = 31.7 × 0.7 = 22.19 A
Active component of I = I cosϕ = I × 0.9 = 0.9I A
These components are represented by OA
0.9I = 22.19
Reactive component of IM = IM sinϕM = 
Reactive component of I = I sinϕ = 
Now, IC = Reactive component of IM – Reactive component of I
= 22.63 – 10.74 = 11.88 A
⇒ 11.88 = 400 × 2π × 50 × c
⇒ c = 94.58 μF
A supply system feeds the following loads
(i) A lighting load of 500 kW
(ii) A load of 400 kW at a p.f. 0.707 lagging
(iii) A load of 800 kW at a p.f. 0.8 leading
(iv) A load of 500 kW at a p.f. 0.6 lagging
(v) A synchronous motor driving a 540 kW d.c. generator and having an overall efficiency of 90%
Calculate the power factor of the synchronous motor so that station power factor may become unity.
(i) The light load works at unity power factor.
P1 = 500 kW, Q1 = 0 KVAR
(ii) P2 = 400 kW, cosϕ2 = 0.707 lagging
Q2 = P2 tanϕ2 = 400 × tan cos-1 (0.707) = 400 KVAR (lagging)
(iii) P3 = 800 kW, cosϕ3 = 0.8 leadingQ3 = P3 tanϕ3 = 800 × tan cos-1(0.8) = 600 KVAR (leading)
(iv) P4 = 500 kW, cosϕ4 = 0.6 lagging
Q4 = P4 tanϕ4 = 500 × tan cos-1(0.6) = 666.67 KVAR (lagging)
Leading KVAR to be taken by synchronous motor
Q5 = Q4 + Q2 – Q3
Q5 = 400 + 666.67 – 600 = 466.66 KVAR
Cosϕ5 = 0.789 leading
|
22 docs|274 tests
|
|
22 docs|274 tests
|
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
