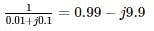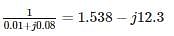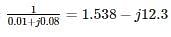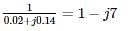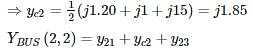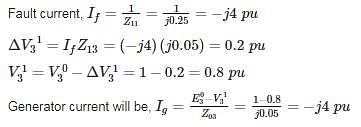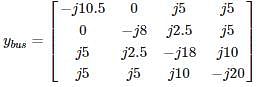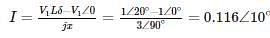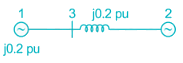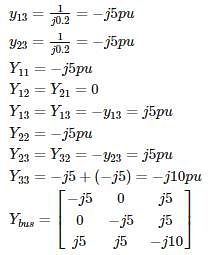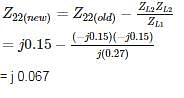Test: Power Systems- 5
10 Questions MCQ Test GATE Electrical Engineering (EE) 2023 Mock Test Series | Test: Power Systems- 5
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A power system has 200 busses including 15 generator buses. For the load flow analysis using the Newton-Raphson method in polar coordinates, the size of the Jacobian is
Total number of buses (n) = 200
Number of generator buses = 15
One generator bus acts as slack bus.
Size of Jacobian = (2 × 200) - 2 - 14
= 384
The Zbus of a system is
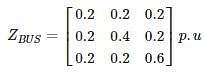
If a 3 phase fault occurs at BUS – 2, the p.u. fault current in each phase is – (in pu)
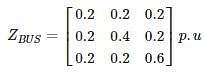
If a 3 phase fault occurs at BUS – 2, the p.u. fault current in each phase is – (in pu)
Three phase fault current is given by
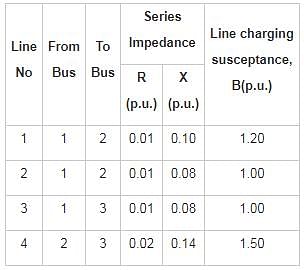
A single line diagram of a power system is shown in the figure. The per unit values of line impedances are given. The sum of diagonal elements of YBUS matrix is
Z12 = j0.18 pu ⇒ y12 = -j10 pu
Z13 = j0.25 pu ⇒ y13 = -j4 pu
Z23 = j0.2 pu ⇒ y23 = -j5 pu
Y11 = y12 + y13 = -j14 pu
Y22 = y21 + y23 = -j15 pu
Y33 = y31 + y32 = -j9 pu
Sum of diagonal elements = -j14 – j15 – j9
= -j38 pu
The power system network is having a 60 bus system. The YbusYbus of this power system network is having 70% of sparse. The minimum number of transmission lines that exist in the bus system___
Total elements in Ybus = 60 × 60 = 3600
Non – zero = 0.3 × 3600 = 1080
Diagonal = 60
Mutual elements = 660
Transmission lines =1020/2=510
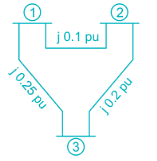
The single line diagram of a power system network having 3 buses and 4 lines is shown in the figure below. The line data is provided in the associated table. The values of the (2, 2) and (2,1) elements of the bus admittance matrix (YBUS) are
From the table
Impedance of line 1 = 0.01 + j0.01
Admittance of line 1 = 
Impedance of line 2 = 0.01 + j0.08
Admittance of line 2 = 
Resultant admittance between the bus1 and bus2
y21 = y12 = 0.99 – j9.9 + 1.538 – j 12.3
= 2.528 – j22.2
Impedance of line 3 = 0.01 + j0.08
Admittance of line 3 = 
y13 = 1.538 – j12.3
Impedance of line 4 = 0.02 + j0.14
Admittance of line 4 = 
Charging susceptance at bus2
2yc2 = sum of charging susceptance of line 1, 2 and
= 2.528 - j22.2 + j1.85 + 1 - j7
= 3.528 – j 27.35
YBUS(2,1) = - y21
= - 2.528 + j22.2
For a Z bus system Z11 = j0.25,Z12 = j0.02,Z13 = j0.05,z14 = j0.04
There are 2 generators at bus 1 and 3 and their sub-transient reactance was induced while calculating Z bus. A three-phase fault occurs at bus 1. The magnitude of pu current supplied by generator 3 whose sub-transient reactance is j0.05 pu is___ (in pu)
The bus admittance matrix for the network shown in the figure is
After converting the given impedances into admittances,
y11 = -j0.5 - j5 - j5 = -j10.5
y22 = -j0.5 - j2.5 - j2.5 = -j5 = -j8.0
y33 = -j0.5 - j5 - j10 - j2.5 = -j18.0
y44 = -j5 - j10 - j5 = -j20.0
y12 = y21 = 0
y13 = y31 = j5.0
y14 = y41 = j5.0
y23 = y32 = j2.5
y24 = y42 = j5.0
y34 = y43 = j10.0
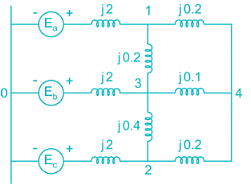
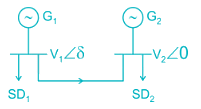
Two generators G1 and G2 are connected with cable having a reactance of j3 PU and the load demand at two buses are SD1 = 20 + j20 PU and SD2 = 25 + j2.5 PU the total reactive power in PU at the generating station G1 when δ = 20° is ______ PU
S = V1I* = 1∠20° × .116∠-10 = 0.116∠10
S1 = SD1 + s
= 20 + 20j + .114 + 0.020j
S1 = 20.114 + 20.02 j
Total power = Active power + Reactive power
∴ Reactive power = 20.02 PU
A generator is connected to an infinite bus through a double circuit line as shown
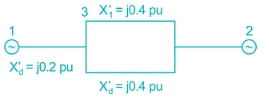
The admittance matrix Y is given by
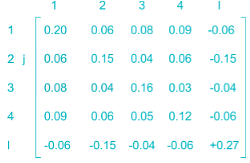
The bus impedance matrix of a 4 – bus power system network is given by
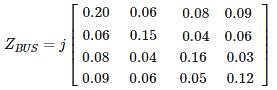
An element having an impedance of j 0.12 pu is connected b/n ref bus and bus 2. Calculate new value of Z22.
|
22 docs|274 tests
|
|
22 docs|274 tests
|
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
