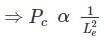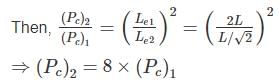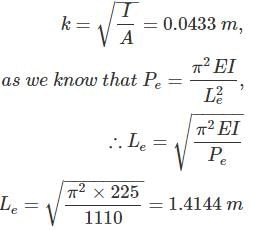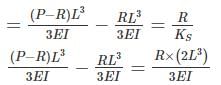Test: Solid Mechanics- 4 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Solid Mechanics- 4
In a closed coiled helical spring, the maximum shear stress occurs on the
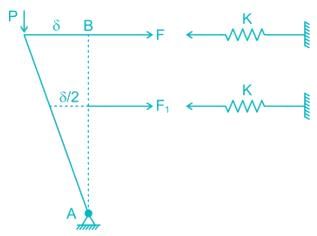
A rigid bar AB of length ‘L’ is supported by a hinge and two springs of stiffness ‘K’ as shown in figure. The buckling load Pcr for the bar will be-

If 10 coils of spring cut out from a spring of 25 coils, then the stiffness of new spring will be
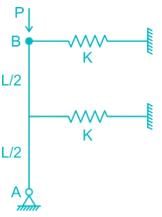
A bar of length L is supported by springs of stiffness Coefficient kA, kB, and a Torsional spring of torsional stiffness coefficient kT as shown in the figure below. The critical load is
A column has a rectangular section of 10 mm x 20 mm & effective length of 1 m. The value of buckling stress (in MPa) is, given that E=200 GPa
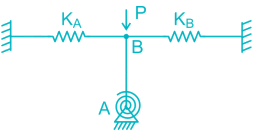
A weight of 40 N falls from a height of 200 mm on a rigid massless bar supported by two identical springs as shown in the figure. If the maximum deflection is 20 mm then the stiffness of spring (in N/mm) is ………..
The euler’s crippling load for a column whose one end is fixed and other free is 60 kN. If one end is made fixed and other hinged, then the crippling load will
An a aluminium column of square cross-section (10 mm × 10 mm) and length 300 mm has both ends pinned. This is replaced by a circular cross-section (of diameter 10 mm) column of the same length and made of the same material with the same end conditions. The ratio of critical stresses for these two columns corresponding to Euler’s critical load, (σcritical)square : (σcirtical)circular’ is
A column has a rectangular cross section of 40 cm × 15 cm and of flexural rigidity 225 Nm2. If the column gets buckle under the axial load of 1110 N. Calculate the slenderness ratio of the column.
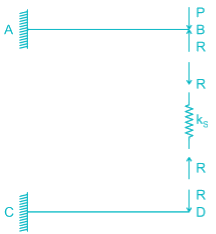
Two beams are connected by a linear spring as shown in the following figure. For a load P as shown in the figure, the percentage of the applied load P carried by the spring is _______________.




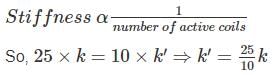
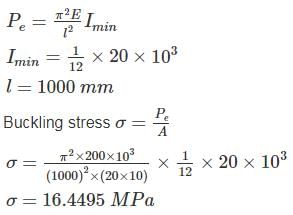
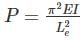
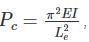 where Le = effective length of column
where Le = effective length of column