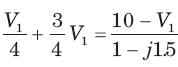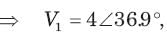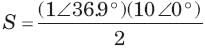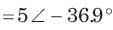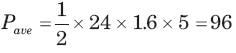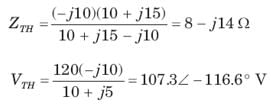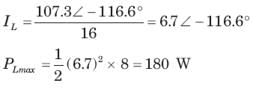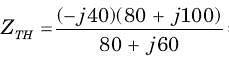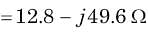Test: Sinusoidal Steady State Analysis - Electronics and Communication Engineering (ECE) MCQ
20 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Sinusoidal Steady State Analysis
In a two element series circuit, the applied voltage and the resulting current are v(t) = 60 + 66sin (10 t) V, i(t) = 2.3sin (103t + 68.3o) A.The nature of the elements would be
Determine the complex power for hte given values in question.
P = 269 W, Q = 150 VAR (capacitive)
Determine the complex power for hte given valuesin question.
Q = 2000 VAR, pf =09. (leading)
Determine the complex power for hte given values in question.
S = 60 VA, Q = 45 VAR (inductive)
Determine the complex power for hte given values in question.
Vrms = 220 V, P = 1 kW, |Z| = 40Ω (inductive)
Determine the complex power for hte given values in question
Vrms = 21∠20°V, Vrms = 21∠20°V, Irms = 8.5∠-50°A
Determine the complex power for hte given values in question.
Vrms = 120∠30°V, Z = 40 + j80Ω
In a two element series circuit, the applied voltage and the resulting current are v(t) = 60 + 66 sin (1000t) V, i(t) = 2.3sin (1000t + 68.3) 3 A. The nature of the elements would be
A relay coil is connected to a 210 V, 50 Hz supply. If it has resistance of 30Ω and an inductance of 0.5 H, the apparent power is
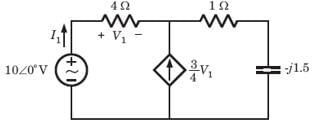
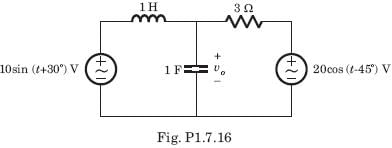
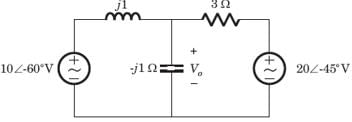
In the circuit shown in fig. power factor is
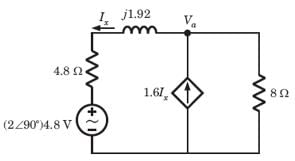
The power factor seen by the voltage source is
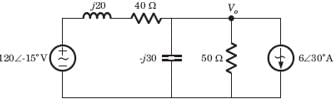
The average power supplied by the dependent source is
In the circuit of fig. the maximum power absorbed by ZL is
The value of the load impedance, that would absorbs the maximum average power is
|
25 docs|263 tests
|


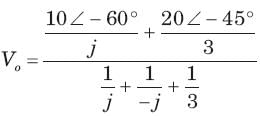
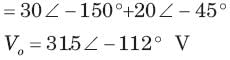

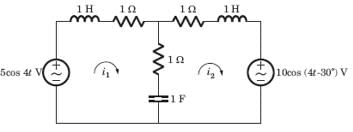
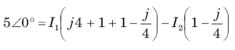
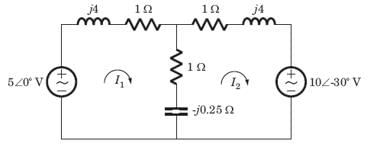
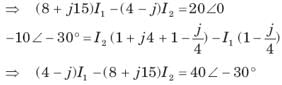
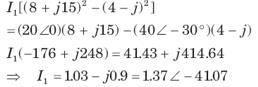
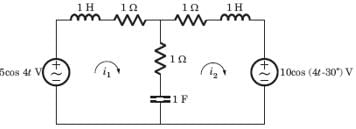
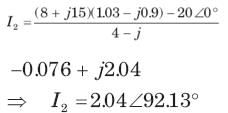
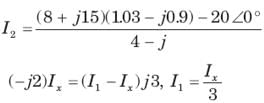
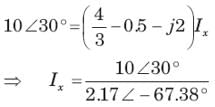
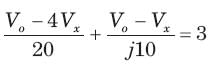
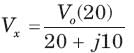
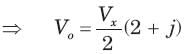
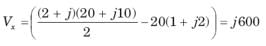
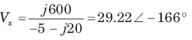
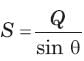
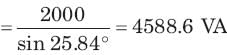
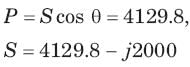
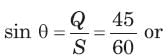
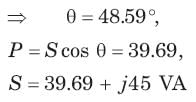
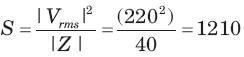
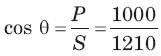 = 0.8264 or θ = 34.26°,
= 0.8264 or θ = 34.26°,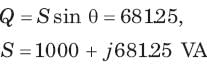
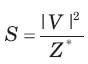
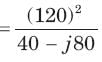 = 72 + j144 VA
= 72 + j144 VA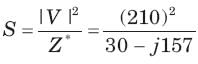
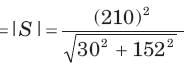 = 275.6 VA
= 275.6 VA