Test: Context-Free Grammars & Push-Down Automata - Computer Science Engineering (CSE) MCQ
30 Questions MCQ Test - Test: Context-Free Grammars & Push-Down Automata
Consider the following languages.
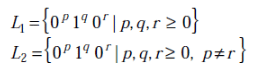
Q. Which one of the following statements is FALSE?
Which of the following pairs have DIFFERENT expressive power?
Let P be a regular language and Q be context-free language such that 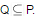 (For example, let P be the language represented by the regular expression p*q* and Q be {pnqn|
(For example, let P be the language represented by the regular expression p*q* and Q be {pnqn| }). Then which of the following is ALWAYS regular?
}). Then which of the following is ALWAYS regular?
Consider the language L1,L2,L3 as given below.
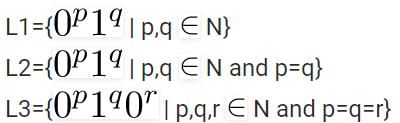
Which of the following statements is NOT TRUE?
Consider the languages L1 = {0i1j | i != j}. L2 = {0i1j | i = j}. L3 = {0i1j | i = 2j+1}. L4 = {0i1j | i != 2j}.
S -> aSa|bSb|a|b; The language generated by the above grammar over the alphabet {a,b} is the set of
Let L = L1 ∩ L2, where L1 and L2 are languages as defined below:
L1 = {ambmcanbn | m, n >= 0} L2 = {aibjck | i, j, k >= 0}
Then L is
The language L= {0i21i | i≥0 } over the alphabet {0,1, 2} is:
Consider the CFG with {S,A,B) as the non-terminal alphabet, {a,b) as the terminal alphabet, S as the start symbol and the following set of production rules
Q. Which of the following strings is generated by the grammar?
For the correct answer strings to above question, how many derivation trees are there?
Here, wr is the reverse of the string w. Which of these languages are deterministic Context-free languages?
Consider the following statements about the context free grammar
G = {S → SS, S → ab, S → ba, S → Ε}
I. G is ambiguous
II. G produces all strings with equal number of a’s and b’s
III. G can be accepted by a deterministic PDA.
Q. Which combination below expresses all the true statements about G?
Which one of the following grammars generates the language L = {aibj | i ≠ j}
In the correct grammar of above question, what is the length of the derivation (number of steps starring from S) to generate the string albm with l ≠ m?
Consider the languages:
L1 = {anbncm | n, m > 0} L2 = {anbmcm | n, m > 0}
Q. Which one of the following statements is FALSE?
Consider the languages:
L1 = {wwR |w ∈ {0, 1}*}
L2 = {w#wR | w ∈ {0, 1}*}, where # is a special symbol
L3 = {ww | w ∈ (0, 1}*)
Q. Which one of the following is TRUE?
The language {am bn Cm+n | m, n ≥ 1} is
If the strings of a language L can be effectively enumerated in lexicographic (i.e., alphabetic) order, which of the following statements is true ?
Let G = ({S}, {a, b} R, S) be a context free grammar where the rule set R is S → a S b | SS | ε Which of the following statements is true?
The language accepted by a Pushdown Automation in which the stack is limited to 10 items is best described as
Which of the following statements is true?
Consider the NPDA 〈Q = {q0, q1, q2}, Σ = {0, 1}, Γ = {0, 1, ⊥}, δ, q0, ⊥, F = {q2}〉, where (as per usual convention) Q is the set of states, Σ is the input alphabet, Γ is stack alphabet, δ is the state transition function, q0 is the initial state, ⊥ is the initial stack symbol, and F is the set of accepting states, The state transition is as follows:
Q. Which one of the following sequences must follow the string 101100 so that the overall string is accepted by the automaton?
Which of the following languages are context-free?
L1 = {ambnanbm ⎪ m, n ≥ 1}
L2 = {ambnambn ⎪ m, n ≥ 1}
L3 = {ambn ⎪ m = 2n + 1}
Which one of the following statements is FALSE?
If we use internal data forwarding to speed up the performance of a CPU (R1, R2 and R3 are registers and M[100] is a memory reference), then the sequence of operations.
Consider the following context-free grammars:
Consider the pushdown automaton (PDA) below which runs over the input alphabet (a, b, c). It has the stack alphabet {Z0, X} where Z0 is the bottom-of-stack marker. The set of states of the PDA is (s, t, u, f} where s is the start state and f is the final state. The PDA accepts by final state. The transitions of the PDA given below are depicted in a standard manner. For example, the transition (s, b, X) → (t, XZ0) means that if the PDA is in state s and the symbol on the top of the stack is X, then it can read b from the input and move to state t after popping the top of stack and pushing the symbols Z0 and X (in that order) on the stack.
Consider the following languages.
L1 = {ai bj ck | i = j, k ≥ 1}
L1 = {ai bj | j = 2i, i ≥ 0}
Q. Which of the following is true?
Consider a CFG with the following productions. S → AA | B A → 0A | A0 | 1 B → 0B00 | 1 S is the start symbol, A and B are non-terminals and 0 and 1 are the terminals. The language generated by this grammar is














