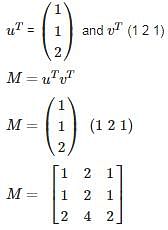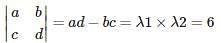Test: Engineering Mathematics- 3 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Engineering Mathematics- 3
The matrix 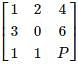 has one eigenvalue equal to 3. The sum of the other two eigenvalues is
has one eigenvalue equal to 3. The sum of the other two eigenvalues is
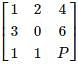 has one eigenvalue equal to 3. The sum of the other two eigenvalues is
has one eigenvalue equal to 3. The sum of the other two eigenvalues isWhat is the determinant of matrix X if 4 and (2 + 7i) are the eigenvalues of X where i = √−1?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In the given matrix one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are
one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are
 one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are
one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 areWhich of the below-given statements is/are true?
I. The eigenvalue of the lower triangular matrix is just the diagonal elements of the matrix.
II. The product of the eigenvalue of a matrix is equal to its trace.
III. If 1/λ is an eigenvalue of A’(inverse of A) then orthogonal of A also have 1/λ as its eigenvalue.
Consider the following 2 × 2 matrix A where two elements are unknown and are marked by a and b. The eigenvalues of this matrix are - 1 and 7. What are the values of a and b?

Let A be the 2 X 2 matrix with elements a11 = 2, a12 = 3, a21 = 1 and a22 = 4 then the Characteristic Equation:?
The latent values of the matrix
 are 1, 1, 2 and the number of linearly independent latent vectors for the repeated root 1 is –
are 1, 1, 2 and the number of linearly independent latent vectors for the repeated root 1 is –
Consider a Matrix M = uTvT where u = (112) and v = 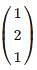 also uT denotes the transpose of matrix u. Find the largest eigenvalue of M?
also uT denotes the transpose of matrix u. Find the largest eigenvalue of M?
What is the absolute difference of the eigenvalues for the matrix 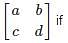 ad – bc = 6 and a + d = 7?
ad – bc = 6 and a + d = 7?
Consider the matrix  which one of the following statements is TRUE for the eigenvalues and eigenvectors of the matrix?
which one of the following statements is TRUE for the eigenvalues and eigenvectors of the matrix?
|
55 docs|215 tests
|
|
55 docs|215 tests
|


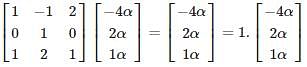


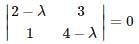
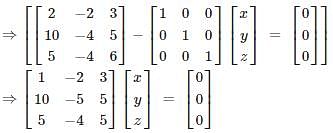
 i.e. one linearly independent latent vector.
i.e. one linearly independent latent vector.