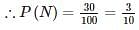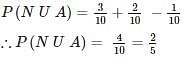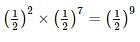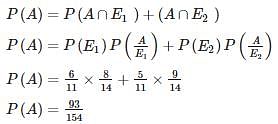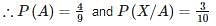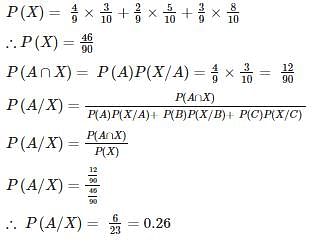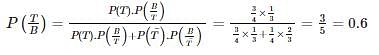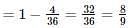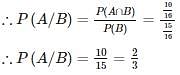Test: Engineering Mathematics- 7
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2023 Mock Test Series | Test: Engineering Mathematics- 7
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
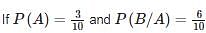where A and B are exhaustive events, then find P(B)?
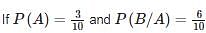where A and B are exhaustive events, then find P(B)?Since A and B are exhaustive events
∴ P(A∪B) = 1
In an examination, 20% of the students have failed in Computer Networks, 30% of the students have failed in Computer Architecture and 10% in Computer Networks and Computer Architecture. If a student is selected at random, then what is the probability that the student has failed in at least one subject?
Let the number of students be 100.
P(N)→ probability that students failed in Computer Networks
P(A)→ probability that students failed in Computer Architecture
P(N∩A)→ probability that the student has failed in both the subject
P(NUA)→ probability that the student has failed in atleast one subject
P(NUA) = P(N) + P(A) − P(N∩A)
A coin is tossed 9 times. What is the probability that the outcome of only first two tosses is headed?
Required probability = 
A pair of dice is thrown. Find the probability of obtaining a sum of 8 or getting an even number on both the dice.
Let the events be defined as:
A: Obtaining a sum of 8
B: Getting an even number on both dice
P(A U B) = P(A) + P(B) – P (A ∩ B)
Now cases favourable to A are (3, 5) (5, 3) (2, 6) (6, 2) (4, 4)
So, P(A) = 5/36
Cases favourable to B: (2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 2), (6, 4), (6, 6).
P(B) = 9/36
Now, (2, 6) (6, 2) and (4, 4) are common to both events A and B
So, P (A ∩ B) = 3/36
⇒ P (A ∪ B) = (5/36) + (9/36) – (3/36) = 11/36
A bag contains 6 red, 5 blue balls, and another bag contains 5 red and 8 blue balls. A ball is drawn from the first bag without noticing the color is put in the second bag. A ball is drawn from the second bag. Find the probability that ball drawn is blue in color.
P(A)→ probability of getting a blue ball from the 2nd bag.
P(E1)→ probability of getting a red ball from the 1st bag.
P(E2)→ probability of getting a blue ball from the 1st bag.
The chances of A, B, C becoming managers of a Testbook company are 4:2:3. The probability that the bonus scheme will be introduced if A, B, C become manager are 0.3, 0.5, 0.8 respectively.
If the bonus scheme has introduced, what is the probability that A is appointed as the manager of Testbook (answer up to 2 decimal place)?
P(X)→ probability that bonus scheme is introduced
P(A) → probability of A being a manager.
P(B) → probability of B being a manager.
P(C) → probability of C being a manager.
P(X) = P (A ∩ X) + P (B ∩ X) + P (C ∩ X)
P(X) = P(A)P(X/A) + P(B)P(X/B) + P(C)P(X/C)
A speaks truth 3 out of 4 times. There is a chance that match can be won, drawn or lost but A reported that Shyam has won the match. Find the probability that his report was correct.
T: A speaks truth ⇒ P(T) = ¾
T̅ : A lies ⇒ P(T̅) = 1 - P(T) = ¼
There are three cases for matches. It can be won, drawn or lost.
The probability of winning a match, P (B/T) = 1/3
The probability of not winning a match, P(B,T̅) = 2/3
Using Baye’s theorem:
A and B throw a pair of dice alternately. A wins if he throws faces with sum 5 before B throws faces with the sum of 6 and B wins if he throws faces with the sum of 6 before A throw faces with the sum of 5. If A begins, the chances of winning for A is________.
The sum 5 can be obtained as follows:
(1, 4), (2, 3), (3, 2), (4, 1)
The probability of A is throwing 5 with two dice is
= 4/36 = 1/9
The probability of A is not throwing 5 is
The sum 6 can be obtained as follows:
(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)
The probability of B is throwing 6 is
= 5/36
The probability of B is not throwing 6 is
Given that A begins,
Now A can win if he throws 5, in first chance,
(or) third Chace (b) fifth chance etc –
The chances of winning of A
An anti-aircraft gun can take a maximum of 4 shots at an enemy plane moving away from it. The probabilities of hitting the plane at the first, second, third and fourth shot are 0.4, 0.3, 0.2 and 0.1 respectively. The probability that the gun hits the plane is_____
Let p1 = 0.4, p2 = 0.3, p3 = 0.2 and p4 = 0.1
P(the gun hits the plane) = P(the plane is hit at least once)
= 1 – P(the plane is hit in none of the shots)
= 1− (1−p1) (1−p2) (1−p3) (1−p4)
= 1− (0.6 × 0.7 × 0.8 × 0.9)
= (1− 0.3024) = 0.6976
What is the probability of getting more than one tail given that at least one coin is head when 4 coins are tossed?
P(A)→ probability of getting more than one tail
∴ P(A) = 11/16
P(B)→ probability of getting at least one tail
∴ P(B) = 15/16
P(A ∩ B)→ probability of getting more than one tail and at least one is head.
∴ P(A ∩ B) = 10/16
|
150 docs|215 tests
|
|
150 docs|215 tests
|
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
