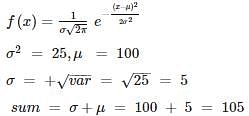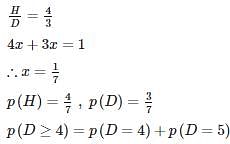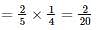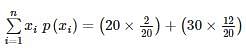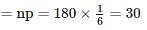Test: Engineering Mathematics- 8
10 Questions MCQ Test RRB JE for Computer Science Engineering | Test: Engineering Mathematics- 8
Given X ¬ B (n,p) if E(X) = 6, Var(X) = 4.2 then what is the value of n?
The probability density function of the normal distribution of a random variable X is
What is the sum of mean and standard deviation?
What is the sum of mean and standard deviation?
Probability density function of normal distribution is
Note:
σ = standard deviation
σ2 = variance
μ = mean
Binomial distribution B(n,p) can be approximated to a normal distribution N(np, np(1−p)) if ____
Binomial distribution B(n,p) can be approximated to normal distribution N(np,np(1−p)) if n is large and p and 1-p are almost equal. Approximation generally improves as n increases (at least 20) and is better when p is not near to 0 or 1.
If a random variable x satisfies the Poisson’s distribution with a mean value of 3, then the probability that (x ≥ 2) is Poisson’s distribution,
For Poisson’s distribution,
Let Harsh and Dinesh be the two players playing chess and their chances of winning a game are in the ration 4:3 respectively. What is the chance of Dinesh winning at least 4 games out of five games played?
From an urn containing 3 red and 2 white balls, a man is to draw 2 balls at random without replacement, being promised Rs. 20 for each red ball he draws and Rs. 10 for each white one. Find his expectation (In rupees).
A man is to draw 2 balls at random without replacement.
Probability to draw 2 red balls 
Probability to draw 2 white balls 
Probability to draw one red ball and one white ball = 
Let X be the random variable and it shows the money he earn.
Expectation = 
If the probability of passing an exam is 0.001, then determine the chance that more than 3 students out of 3,000 will pass the exam (answer up to 2 decimal place)?
Poisson distribution is used as probability of occurrence is very small.
mean = λ = n
∴ λ = 3000 × 0.001 = 3
= 0.35
A dice is rolled 180180 times, find the probability that face 44 will turn up at least 3535 times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413
Given that n = 180
Required Probability is given by 
∴ mean 
Variance = npq = 25
= 0.5 – 0.3413 = 0.1587
The probability that GATE CS/IT question has an error is 1/20 and 65 questions are made in such an exam. If the probability that at least 2 question has an error is [1−[a(19/20)64]] then what is the value of a (answer up to 2 decimal place)?
Using Binomial Distribution
Probability that x questions have an error
If X is a Poisson variate such that P(X=2) = 3P(X=4) then what is the value of P(X=3)?
P (X = 2) = 3P (X = 4)
 |
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
Recommended Content
 |
|
 |
|
 |
|
 |
|
 |
|
Recommended Tests
 |
|
|
|
|
|
|
|
|
|
Download free EduRev App
Similar Content
 |
|
 |
|
 |
|
 |
|
Related tests
|
|
|
|
|
|
|
|
|
|
|
© EduRev
|
Follow Us
|