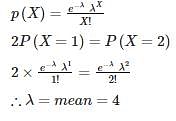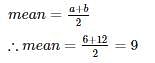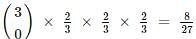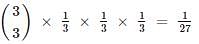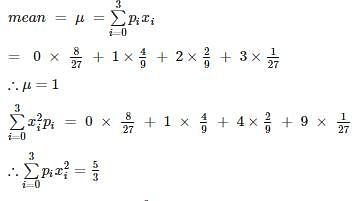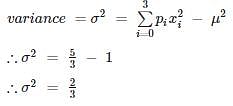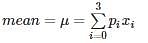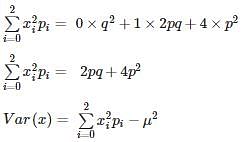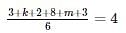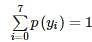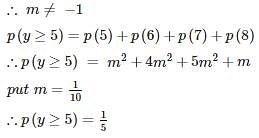Test: Engineering Mathematics- 9 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Engineering Mathematics- 9
A sample of 15 data is as follows: 17, 18, 17, 17, 13, 18, 5, 5, 6, 7, 8, 9, 20, 17, 3. the mode of the data is
In a Poisson distribution if 2P(X = 1) = P(X = 2), then what is the mean?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The continuous distribution variable X is distributed uniformly where X ~ U(6,12). Find the mean of X?
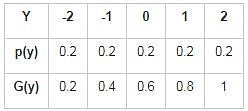
Consider a discrete random variable Y that takes values -2, -1, 0, 1, and 2 with probability 0.2 each. The values of the cumulative distribution function G(y) at y = -1 and y = 1 are _____ and _____ respectively.
A die is tossed thrice. Success is getting 2 or 5 on a toss. What is the variance of the number of success?
What is the variance of the random variable X whose probability mass function is given below?

3, k, 2, 8, m, 3
The arithmetic mean of the list of numbers above is 4. If k and m are integers and k ≠ m, what is the median of the list?
If a random variable X has a Poisson distribution with variance 6, then expectation [E(X + 3)2] equals _____.
The probability density function of a random variable function y has the following probability function:
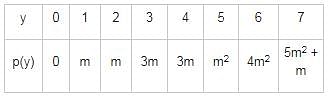
find p(y ≥ 5)?
In a binomial distribution, the mean is 4 and variance is 3. Then the mode is
|
55 docs|215 tests
|
|
55 docs|215 tests
|