Test: K Map & Logic Gates - Computer Science Engineering (CSE) MCQ
30 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: K Map & Logic Gates
Consider numbers represented in be the Gray code representation of a number n and let
be the Gray code representation of a number n and let  be the Gray code of
be the Gray code of  value of the number .Which one of the following functions is correct?
value of the number .Which one of the following functions is correct?
For any natural number , an ordering of all binary strings of length n is a Gray code if it starts with 0n, and any successive strings in the ordering differ in exactly one bit (the first and last string must also differ by one bit). Thus, for n = 3, the ordering (000, 100, 101, 111, 110, 010, 011, 001) is a Gray code. Which of the following must be TRUE for all Gray codes over strings of length n?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
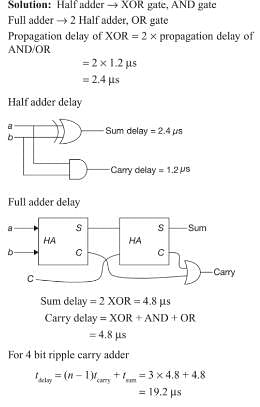
A half adder is implemented with XOR and AND gates. A full adder is implemented with two half adders and one OR gate.
The propagation delay of an XOR gate is twice that of an AND/OR gate. The propagation delay of an AND/OR gate is 1.2 microseconds. A 4-bit-ripple-carry binary adder is implemented by using four full adders. The total propagation time of this 4-bit binary adder in microseconds is ______.
The propagation delay of an XOR gate is twice that of an AND/OR gate. The propagation delay of an AND/OR gate is 1.2 microseconds. A 4-bit-ripple-carry binary adder is implemented by using four full adders. The total propagation time of this 4-bit binary adder in microseconds is ______.
Consider the binary code that consists of only four valid codewords as given below: 00000, 01011, 10101, 11110
Let the minimum Hamming distance of the code p and the maximum number of erroneous bits that can be corrected by the code be q. Then the values of p and q are
In the IEEE floating point representation the hexadecimal value corresponds to
The following bit pattern represents a floating point number in IEEE 754 single precision format
1 10000011 101000000000000000000000
The value of the number in decimal form is
The decimal value 0.5 in IEEE single precision floating point representation has
A Boolean function f is to be realized only by NOR gates. Its K-map is given below:
The realization is
What is the equivalent Boolean expression in product-of-sums form for the Karnaugh map given in Fig
Which of the following expressions is in the product-of-sums form?
Which of the following functions implements the Karnaugh map shown below?
The prime implicant which has at least one element that is not present in any other implicant is known as
Given the following karnaugh map, which one of the following represents the minimal Sum-Of-Products of the map?
Minimum sum of product expression for f(w,x,y,z) shown in Karnaugh-map below
The boolean function for a combinational circuit with four inputs is represented by the following Karnaugh map.
Which of the product terms given below is an essential prime implicant of the function?
Consider the following expression
Which of the following Karnaugh Maps correctly represents the expression?
Consider the following expression
Which of the following expressions does not correspond to the Karnaugh Map obtained for the given expression?
In the Karnaugh map shown below, X denotes a don’t care term. What is the minimal form of the function represented by the Karnaugh map?
What is the minimal form of the Karnaugh map shown below? Assume that X denotes a don’t care term
Consider the Karnaugh map given below, where X represents "don't care" and blank represents 0.
Assume for all inputs the respective complements
are also available. The above logic is implemented using 2-input NOR gates only. The minimum number of gates required is ____________ .
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only:
All digital circuits can be realized using only
Which one of the following circuits is NOT equivalent to a 2-input XNOR (exclusive NOR) gate?
The Boolean function obtained by adding an inverter to each and every input of an gate is:
The capacity of a memory unit is defined by the number of words multiplied by the number of bits/word. How many separate address and data lines are needed for a memory of ?
A circuit outputs a digit in the form of 4 bits. 0 is represented by 0000, 1 by 0001, …, 9 by 1001. A combinational circuit is to be designed which takes these 4 bits as input and outputs 1 if the digit > 5, and 0 otherwise. If only AND, OR and NOT gates may be used, what is the minimum number of gates required?
What is the minimum number of NAND gates required to implement a 2-input EXCLUSIVE-OR function without using any other logic gate?
What is the minimum number of gates required to implement the Boolean function (AB+C) if we have to use only 2-input NOR gates?
Consider the following Boolean function of four variables:
The function is
Consider the following Boolean function of four variables
The function is
The simplified SOP (Sum of Product) from the Boolean expression
is
|
55 docs|215 tests
|
|
55 docs|215 tests
|