Test: Normal Forms- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Normal Forms- 1
Relation R is decomposed using a set of functional dependencies, F and relation S is decomposed using another set of functional dependencies G. One decomposition is definitely BCNF, the other is definitely 3NF, but it is not known which is which. To make a guaranteed identification, which one of the following tests should be used on the decompositions? (Assume that the closures of F and G are available).
From the following instance of a relation scheme R (A, B, C), we can conclude that :
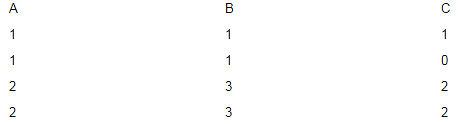
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider a schema R(A,B,C,D) and functional dependencies A->B and C->D. Then the decomposition of R into R1(AB) and R2(CD) is
Suppose the adjacency relation of vertices in a graph is represented in a table Adj(X,Y). Which of the following queries cannot be expressed by a relational algebra expression of constant length?
Let r and s be two relations over the relation schemes R and S respectively, and let A be an attribute in R. then the relational algebra expression is always equal to
R(A,B,C,D) is a relation. Which of the following does not have a lossless join, dependency preserving BCNF decomposition?
Which of the following relational calculus expressions is not safe?
Consider a relation geq which represents “greater than or equal to”, that is, (x,y) ∈ geq only if y >= x.
Q. Which of the following is possible if a tuple (x,y) is deleted?
Given the relations
employee (name, salary, deptno) and department (deptno, deptname, address)
Q. Which of the following queries cannot be expressed using the basic relational algebra operations (U, -, x, , p)?
Given the following relation instance.
Which of the following functional dependencies are satisfied by the instance?
Consider an Entity-Relationship (ER) model in which entity sets E1 and E2 are connected by an m : n relationship R12, E1 and E3 are connected by a 1 : n (1 on the side of E1 and n on the side of E3) relationship R13. E1 has two single-valued attributes a11 and a12 of which a11 is the key attribute. E2 has two single-valued attributes a21 and a22 is the key attribute. E3 has two single-valued attributes a31 and a32 of which a31 is the key attribute. The relationships do not have any attributes. If a relational model is derived from the above ER model, then the minimum number of relations that would be generated if all the relations are in 3NF is ___________.
Consider the relation X(P, Q, R, S, T, U) with the following set of functional dependencies
Q. Which of the following is the trivial functional dependency in F+ is closure of F?
Consider the following entity relationship diagram (ERD), where two entities E1 and E2 have a relation R of cardinality 1 : m.
The attributes of E1 are A11, A12 and A13 where A11 is the key attribute. The attributes of E2 are A21, A22 and A23 where A21 is the key attribute and A23 is a multi-valued attribute. Relation R does not have any attribute. A relational database containing minimum number of tables with each table satisfying the requirements of the third normal form (3NF) is designed from the above ERD. The number of tables in the database is
A relational database contains two tables student and department in which student table has columns roll_no, name and dept_id and department table has columns dept_id and dept_name. The following insert statements were executed successfully to populate the empty tables:
Insert into department values (1, 'Mathematics')
Insert into department values (2, 'Physics')
Insert into student values (l, 'Navin', 1)
Insert into student values (2, 'Mukesh', 2)
Insert into student values (3, 'Gita', 1)
Q. How many rows and columns will be retrieved by the following SQL statement?
Select * from student, department
Consider the entities 'hotel room', and 'person' with a many to many relationship 'lodging' as shown below:
If we wish to store information about the rent payment to be made by person (s) occupying different hotel rooms, then this information should appear as an attribute of
A table has fields Fl, F2, F3, F4, F5 with the following functional dependencies F1 → F3 F2→ F4 (F1 . F2) → F5 In terms of Normalization, this table is in
Which of the following is NOT a superkey in a relational schema with attributes V, W, X, Y, Z and primary key V Y ?
Let R (A, B, C, D, E, P, G) be a relational schema in which the following functional dependencies are known to hold: AB → CD, DE → P, C → E, P → C and B → G. The relational schema R is
Which option is true about the SQL query given below?
SELECT firstName, lastName
FROM Employee
WHERE lastName BETWEEN 'A%' AND 'D%';
|
55 docs|215 tests
|
|
55 docs|215 tests
|

















