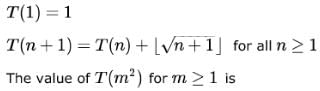Test: Recurrence & Searching- 1
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2023 Mock Test Series | Test: Recurrence & Searching- 1
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
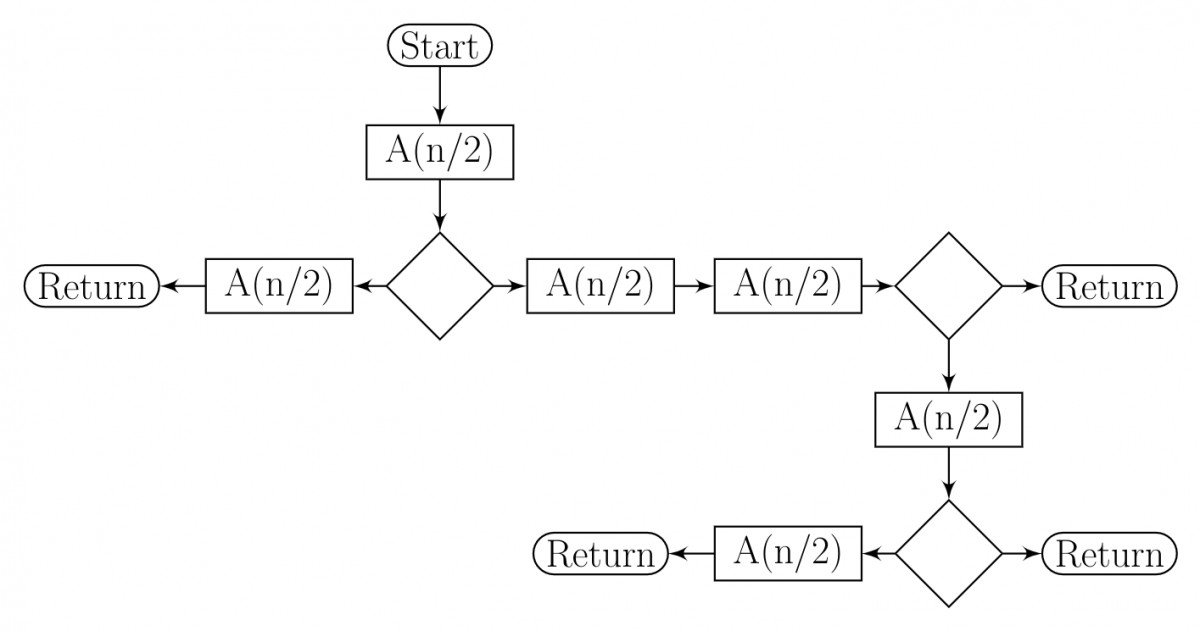
The given diagram shows the flowchart for a recursive function
A(n). Assume that all statements, except for the recursive calls, have
O(1) time complexity. If the worst case time complexity of this function is
O(nα) then the least possible value (accurate up to two decimal positions) of
α is ________.
Flow chart for Recursive Function A(n).
If they are asking for worst case complexity hence,
By calling A(n) we get A(n/2) 5 times,
Hence by applying masters theorem,
Thus value of alpha will be 2.32
The recurrence relation that arises in relation with the complexity of binary search is:
It is B. searching for only one half of the list. leading to T(n/2) + constant time in comparing and finding mid element.
The recurrence relation
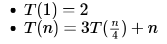
has the solution T (n) equal to
According to Master theorem,
Let
T(n) be the function defined by
Which of the following statements is true?
using master method (case 1)
We can apply Master's theorem case 1 with
So,
So, only option possible is B.
We can also directly solve as follows:
OR
The running time of the following algorithm
Procedure A(n)
If n<=2 return (1) else return 
is best described by:
The complexity will be the number of times the recursion happens which is equal to the number of times we can take square root of n recursively, till n becomes 2.
(We are taking floor of square root of numbers, and between
successive square roots number of numbers are in the series 3,5,7... like 3 numbers from 1...4,5numbers from 5-9 and so on).
We can try out options here or solve as shown at end:
Put
So, answer must be B.
Consider a list of recursive algorithms and a list of recurrence relations as shown below. Each recurrence relation corresponds to exactly one algorithm and is used to derive the time complexity of the algorithm.
Which of the following is the correct match between the algorithms and their recurrence relations?
These are examples of some standard algorithms whose
Merge Sort: T(n) = 2T(n/2) + Θ(n). It falls in case 2 as c is 1 and Logba] is also 1 and the solution is Θ(n Logn) //time complexity can be evaluated using Master Method
Binary Search: T(n) = T(n/2) + Θ(1). It also falls in case 2 as c is 0 and Logba is also 0 and the solution is Θ(Logn) //time complexity can be evaluated using Master Method
Quick Sort : Time taken by QuickSort in general can be written as T(n) = T(k) + T(n-k-1) + 
(n)
Tower of Hanoi : T(n) = 2T(n-1) + 1
Let T(N) be a function defined by the recurrence
Which of the following statements is TRUE?
Option C it can be done by Master theorem.
So,
is true for any real
Hence Master theorem Case 1 satisfied,
|
150 docs|215 tests
|
|
150 docs|215 tests
|
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
