Test: Regular Expressions & Languages- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Regular Expressions & Languages- 1
Which one of the following regular expressions represents the language: the set of all binary strings having two consecutive 0's and two consecutive 1's?
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only.
Let 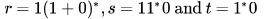 be three regular expressions. Which one of the following is true?
be three regular expressions. Which one of the following is true?
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only: Which of the following regular expression identities is/are TRUE?
In some programming language, an identifier is permitted to be a letter followed by any number of letters or digits. If and denote the sets of letters and digits respectively, which of the following expressions defines an identifier?
Which two of the following four regular expressions are equivalent? (ε is the empty string).
Which one of the following regular expressions over {0,1} denotes the set of all strings not containing as substring?
If the regular set A is represented by A — (01 + 1)* and the regular set B is represented by B — ((01)*1*)*, which of the following is true?
The string 1101 does not belong to the set represented by
Lets' and T be languages over S = {a. b} represented by the regular expressions (a + b*)* and (a + b)*, respectively. Which of the following is true?
The regular expression 0*(10*)* denotes the same set as
Which of the following statements is TRUE about the regular expression 01*0?
Which one of the following regular expressions is NOT equivalent to the regular expression (a + b + c)*?
Which regular expression best describes the language accepted by the non-deterministic automaton below?
Consider the regular expression R = (a + b)* (aa + bb) (a + b)*
Which one of the regular expressions given below defines the same language as defined by the regular expression R?
Which of the following regular expressions describes the language over{0, 1} consisting of strings that contain exactly two 1's?
Which one of the following languages over the alphabet {0,1} is described by the regular expression: (0 + 1)*0(0 + 1)*0(0 + 1)*?
Let has even number of 1s} i.e., L is the set of all the bit strings with even numbers of 1s. Which one of the regular expressions below represents L?
Which of the regular expressions given below represent the following DFA?
Let r,s,t be regular expressions. Which of the following identities is correct?
Which of the following regular expressions correctly accepts the set of all 0/1-strings with an even (poossibly zero) numbe of 1s?



















