CDS I - Mathematics Previous Year Question Paper 2018 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2025 - CDS I - Mathematics Previous Year Question Paper 2018
A man undertakes to do a work in 150 days. He employs 200 men. He finds that only a quarter of the work is done in 50 days. How many additional men should he employ so that the whole work is finished in time?
A train moving with a speed of 60 km per hour crosses an electric pole in 30 seconds. What is the length of train in meters?
Rs. 120 is distributed among A, B and C so that A’s share is Rs. 20 more than B’s and Rs. 20 less than C’s. What is the B’s share?
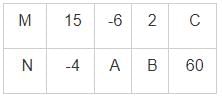
In the following table of inverse variations, what are the values of A, B and C respectively?
A person borrows Rs. 5000 at 5% rate of interest per annum and immediately lent it at 5.5%. After two years he collected the amount and settled his loan. What is the amount gained by him this transaction?
At present the average of the ages of a father and a son is 25 years. After seven years, the son will be 17 years old. What will be the age of father after 10 years?
If 5 tractors can plough 5 hectares of land in 5 days, then what is the number of tractor required to plough 100 hectares in 50 days?
A merchant commences with a certain capital and gains annually at the rate of 25%. At the end of 3 years he has Rs. 10,000. What is the original amount that the merchant invested?
Which of the following decimal number is a rational number with denominator 37?
The annual income of a person decreases by Rs. 64 if the rate of interest decreases from 4% to 3.75%. What is his original annual income?
For 0 < m < 1, which one the following is correct?
A gentleman left a sum of Rs. 39000 to be distributed among his widow, 5 sons and 4 daughters. If each son receives three times as much as a daughter receives, and each daughter receives twice as much as their mother receives, then what is the widow’s share?
Three numbers which are co-prime to each other, are such that the product of the first two 286 and that of the last two is 770. What is the sum of three terms?
The age of a woman is two-digit integer. On reversing this integer, the new integer is the age of her husband who is elder to her. The difference between their ages is one eleventh of their sum. What is the difference between their ages?
A passenger train and a goods train are running in the same direction on parallel railway tracks. If the passenger train now takes three times as long to pass the goods train, as when they are running in the opposite directions, then what is the ratio of the speed of the passenger train to that of the goods train?
All odd prime numbers up to 110 are multiplied together. What is the unit digit in this product?
An alloy A contains two elements, copper and tin in the ratio of 2 : 3, whereas an alloy B contains the same elements in the ratio of 3 : 4. If 20 kg of alloy A, 28 kg of alloy B and some more pure copper are mixed to form a third alloy C which now contains copper and tin in the ratio of 6 : 7, then what is the quantity of the pure copper mixed in the alloy C?
A quadratic polynomial ax2 + bx + c = 0 is such that when it is divided by x, (x - 1) and (x + 1), the remainders are 3, 6 and 4 respectively. What is the value of (a + b)?
If the average of 9 consecutive positive integers is 55, then what is the largest integer?
The average of the ages of 15 students in a class is 19 years. When 5 new students are admitted to the class, the average age of the class becomes 18.5 years. What is the average age of the 5 newly admitted students?
A water tank has been fitted with two taps P and Q and a drain pipe R. Taps P and Q fill at the rate of 12 litres per minute and 10 litres per minute respectively.
Consider the following statements S1, S2 and S3:
S1: Pipe R drains out at the rate of 6 litres per minute
S2: If both the taps and the drain pipe are opened simultaneously, then the tank is filled in 5 hours 45 minutes
S3: Pipe R drains out (fully) the filled tank in 15 hours 20 minutes.
To know what is the capacity of the tank, which one the following is correct?
A man can row at a speed of x km/h in still water. If in a stream which is flowing at a speed of y km/h it takes him z hours to row to a place and back, then what is the distance between the two places?
A car has an average speed of 60 km per hour while going from Delhi to Agra and has an average speed of y km per hour while returning to Delhi from Agra (by travelling the same distance). If the average speed of the car for the whole journey is 48 km per hour, what is the value of y?
An article is sold at a profit of 32%. If the cost price is increased by 20% and the sale price remains the same, then the profit percentage becomes
A, B, C, D and E start a partnership firm. Capital contributed by A is three times that contributed by D. E contributes half of A’s contribution, B contributes one third of E’s contribution and C contributes two third of A’s contribution. If the difference between the combined shares of A, D and E and the combined shares of B and C in the total profit of the firm is Rs. 13500, what is the combined share of B, C and E? (The shares are supposed to be proportional to the contributions)
517 + 518 + 519 + 520 is divisible by
If a + b = 2c, then what is the value of a/(a - c) + c/(b - c)?
If x = y1/a, y = z1/b and z = x1/c where x ≠ 1, y ≠ 1 and z ≠ 1, then what is the value of abc?
If 2b = a + c and y2 = xz, then what is xb - c yc - a za - b‑ equal to?
Which one of the following is correct?
|
33 docs|73 tests
|














