Mathematics Mock Test - 3 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2024 - Mathematics Mock Test - 3
A certain number when divided by 899 leaves the remainder 65. when the same number is divided by 31, the remainder is:
The average weight of 8 person is increased by 2.5 kg when one of them whose weight is 56 kg is replaced by a new man. The weight of the new man is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Last year my age was a perfect square number .next year it will be a cubic number. What is my present age?
4 men can complete a piece of work in 2 days. 4 women can complete the same piece of work in 4 days whereas 5 children can complete the same piece of work in 4 days. If 2 men, 4 women and 10 children work together, in how many days can the work be completed?
A 280 meter long train moving with an average speed of 108 km/h crosses a platform in 12 seconds. A man crosses the same platform in 10 seconds. What is the speed of the man?
The compound interest on a certain sum of money for 2 years at 10% per annum is Rs. 420. Find the simple interest at the same rate and for the same time.
Manoj marked up an article for Rs 15000. Had he offered a discount of 10% on the marked price, he would have earned a profit of 8%. What is the Cost price?
A shopkeeper mixed two verities of rice at Rs. 20/kg and Rs. 30/kg in the ratio 2 : 3 and sell the mixture at 10% profit. Find the price per kg at which he sold the mixture?
Two pipes A and B can fill a tank in 36 hours and 45 hours respectively. If both the pipes are opened simultaneously, how much time will be taken to fill the tank?
In an examination, 34% of the students failed in mathematics and 42% failed in English. If 20% of the students failed in both the subjects, then find the percentage of students who passed in both the subjects.
A jar contains a mixture of 2 liquids A and B in the ratio 4:1. When 10litres of the mixture is taken out and 10 litres of liquid B is poured into the jar, the ratio becomes 2:3. How many litres of the liquid A was contained in the jar?
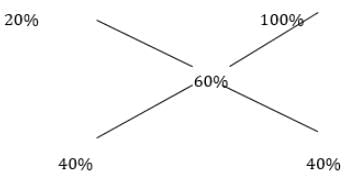
If x + y + z = 0, then what is 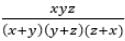 equal to?
equal to?
[x ≠-y , y≠-z , z≠-x]
Two spherical iron shots each of diameter 6 cm are immersed in the water contained in a cylindrical vessel of radius 6 cm. The level of the water in the vessel will be raised by
If the length of a rectangular plot of land is increased by 5% and the breadth decreased by 10% by how much will its area change?
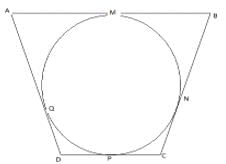
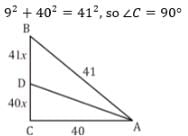
A quadrilateral ABCD circumscribes a circle and AB = 6cm, CD = 5 cm and AD = 7 cm. The length of the sides BC is
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their respective volumes is:
In a ∆ABC, BC=9 cm, AC=40 cm and AB = 41 cm. If bisector of angle A meets side BC at D then ratio of area of ∆ABD ad ∆ABC is -
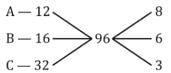
A can complete a work in 12 days, B in 16 days and C in 32 days they start together. A works for 3 days and leaves and B leaves 3 days before the work is finished. In how many days was the work finished?
Find the maximum and minimum value of 8 cosA+15 sinA+15
The simple interest on a sum of money is 13/25 of the sum. If number of years is numerically equal to 1/13 of rate percent per quarter. Then number of years for which the sum as invested is
A milkman bought 60 liters of milk at 10 Rs. per liter and also bought 40 liters of milk at 20 Rs per liter and mixed it. Then he spent 100 Rupees and made 12 kg cream and 96 liter toned milk. He sold cream at 80 Rs. per kg and toned milk at 10 Rupee per liter find his profit percentage
|
23 docs|73 tests
|
|
23 docs|73 tests
|


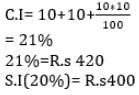

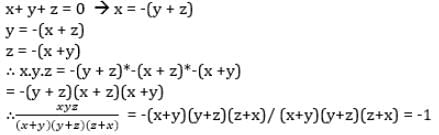
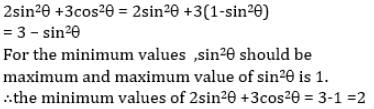
 is equal to
is equal to 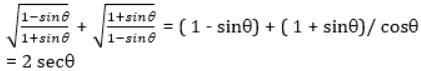
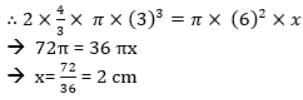
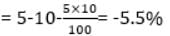
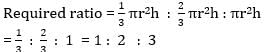

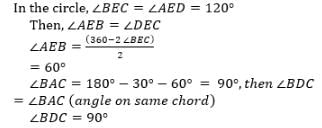

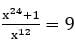 , then the value of
, then the value of 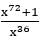 is
is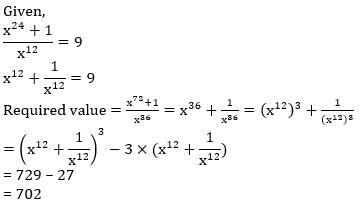
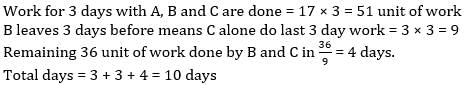
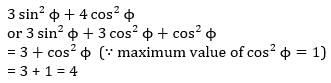
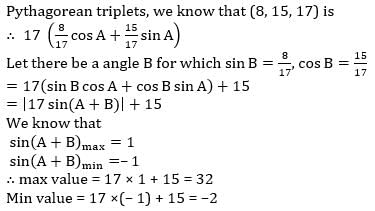
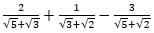 and b =
and b = 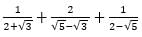
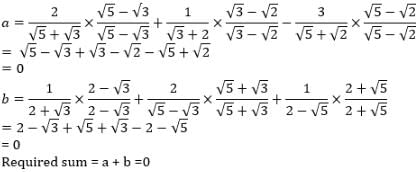
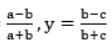 and z =
and z = 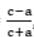 then the value of
then the value of 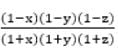 is
is