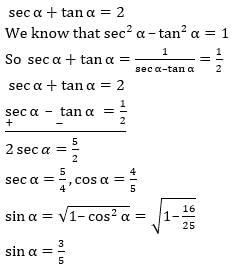Mathematics Mock Test - 4 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2024 - Mathematics Mock Test - 4
If x + y + z = 6 and xy + yz + zx = 11, then the value of x3 + y3 + Z3 - 3xyz is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If α + β+ y = π, then the value of sin2 α + sin2 β — sin2 y, is equal to
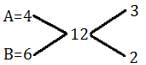
Sum of the digits of a two digit number is 12. When 18 is deduced from the number, the digits change their positions. Find the number.
In an office 80% of the employees are male. Among them 20% are matriculates and remaining are graduates. Among them females 25% are matriculates and the remaining are graduates. If the total numbers of the female employees of the office is 600, how many graduates are in the Office?
The population of a town is 10,000. It increased by 10% during the first year. During the second year, it decreased by 20% and increased by 30% during the third year. What is the population after 3 years?
Copper and zinc are in the ratio 2 : 3 in 200 gms of an alloy. The quantity (in grams) of copper to be added to it to make the ratio 3 : 2 is
The average salary per head of all the workers of an office is Rs. 95. The average salary of 15 officers is Rs. 525 and the average salary of the rest is Rs. 85. Find the total numbers of workers?
By selling oranges at 32 a rupee, a man loses 40%. How many for a rupee should he sell in order to gain 20%?
Two trains P and Q start at the same time in the opposite directions from two points and both the trains after crossing a certain point C arrives at Q and P after  and
and  hours respectively. At what speed is the second train Q running if the first is running at the speed of 8 km/hrs?
hours respectively. At what speed is the second train Q running if the first is running at the speed of 8 km/hrs?
A and B can separately do a work in 20 and 15 days respectively. They worked together for 6 days after which B was replaced by C. If the work is finished in next four days, the number of days in which C alone can do the work will be–
The speeds of three students are in the ratio 2 : 3 : 4. The ratio of the time taken by these students to travel the same distance is
Pipe A can fill a tank in 4 hrs. and pipe B can fill it in 6 hrs. If they are opened on alternative hour, in how many hours the half tank will be filled?
The simple interest on an amount in 2 years at the rate of 7% per year is equal to the simple interest on Rs. 1750 in 4 years at the rate of 5% per year. Find the principal.
At simple interest Rs. 800 becomes Rs. 920 in 3 years. If rate of interest is increased numerically by 3% then the total amount will become–
Two roads of 2 metre width cuts each other perpendicularly in a park of dimension 72m×48m in the middle. Each road is parallel to each side of the rectangle. What is the area of the remaining part of the field?
The area of circle whose radius is 8cm is trisected by two concentric circles. The ratio of radii of the concentric circles in a scending order is
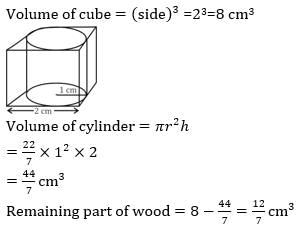
There is a wooden cube of side 2 cm. If a cylinder of maximum volume is cut out from that cube, then what will be the volume of remaining part of the wood?
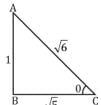
If sin θ + sin2 θ + sin3 θ = 1, then cos6 θ - 4 cos4 θ + 8cos2 θ =?
If cos2 α - sin2 α = tan2 β, then the value of cos2 β - sin2 β is
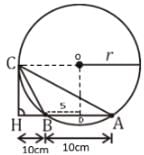
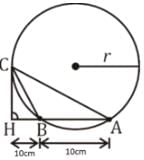
Find radius r (in c.m) of the given circle where CH is tangent to circle & HBA is a secant.
If sec α + tan α = 2, then the value of sin α is — (assume that 00 < α < 90°)
|
23 docs|73 tests
|
|
23 docs|73 tests
|


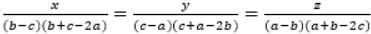 then the value of x + y + z is
then the value of x + y + z is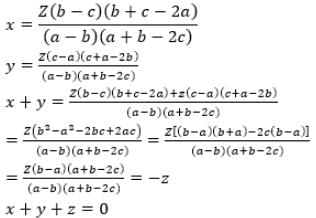
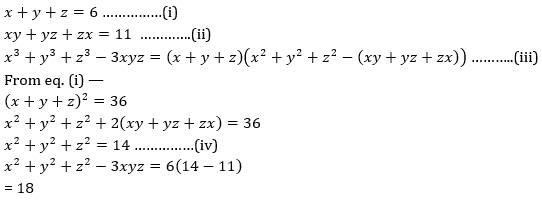
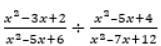 is equal to:
is equal to: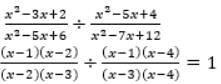
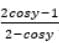 then the value of tan is x/2. cot y/2 is
then the value of tan is x/2. cot y/2 is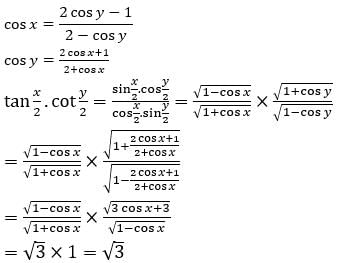
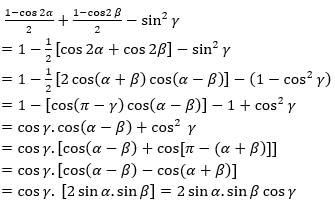
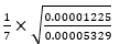 is equal to
is equal to 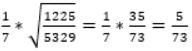
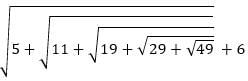 is
is 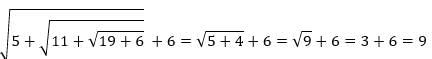
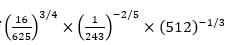 is-
is-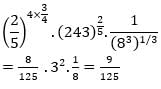
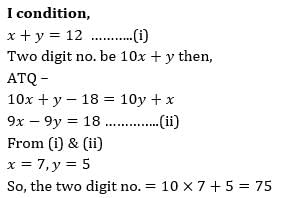

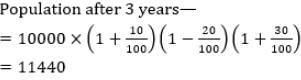
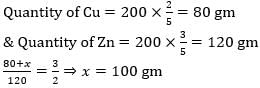
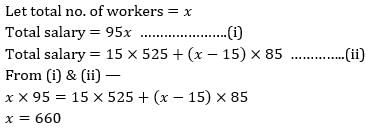


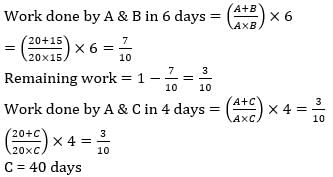
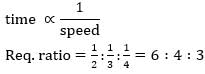
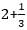 hr
hr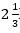 hours.
hours.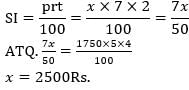
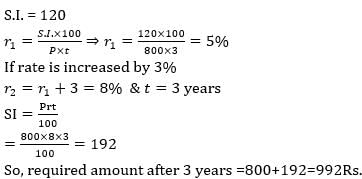
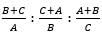 is
is 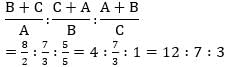


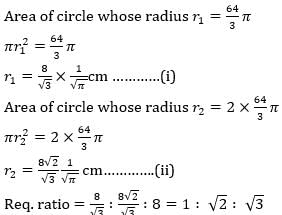
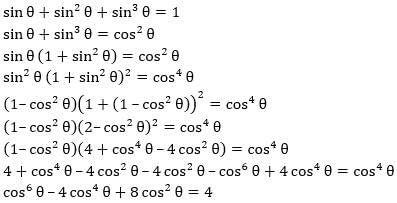
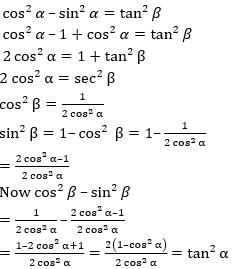
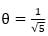 and
and 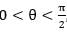 , then the value of
, then the value of 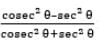 is
is