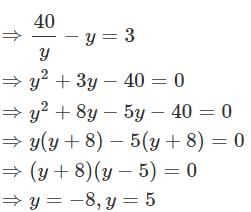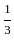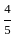Test: Elementary Mathematics - 10 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2024 - Test: Elementary Mathematics - 10
Find the approximate height of the circular cone?
A bag contains Rs. 550 in the form of 50 p, 25 p and 20 p coins in the ratio 2 ∶ 3 ∶ 5. The difference between the amounts that are contributed by the 50 p and the 20 p coins is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
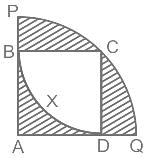
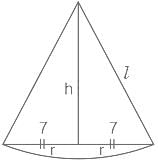
Find the area of the shaded region in the figure given below if the radius of sector CBXD is 20 cm.
 ?
?
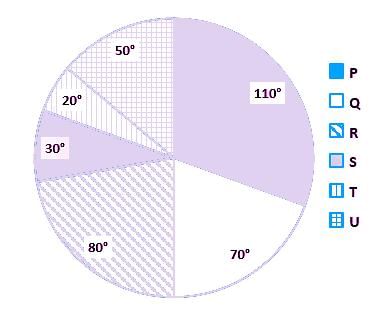
The pie chart given below shows the production of wheat by six states. The total production of wheat by all these six states is 3600. The production of wheat of a particular state is shown in terms of degree with respect to the total production of wheat by all these six states.
What is the difference between average production of wheat by P and Q and the average production of wheat by R and T?
What is the mean deviation of the largest six observations?
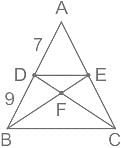
D and E are points on the sides AB and AC, respectively, of ΔABC such that DE is parallel to BC and AD ∶ DB = 7 ∶ 9. If CD and BE intersect each other at F. then find the ratio of areas of ΔDEF and ΔCBF.
What is the variance of the largest six observations?
Determine the nature of the roots of the equation 2x2 + 5x + 5 = 0
If both are moving in the same direction and the submarine is ahead of the warship in both the situations, then the speed of the warship, if the ratio of the speed of warship to that of the submarine is 2 ∶ 1, is:
A man’s basic pay for a 40 hours’ week is Rs. 200. Overtimes is paid at 25% above the basic rate. In a certain week, he worked overtime and his total was Rs. 300. He therefore, worked for a total of (in hours):
The table given below shows the income and expenditure of five companies.
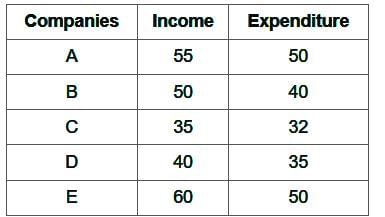
What is the difference between average income and average expenditure of all the companies?
The set of all values of x satisfying the inequation |x - 1| ≤ 5 and |x| ≥ 2, is
A two digit number contains the smaller of two digits in the units place. The product is 40 and the difference between the digits is 3. Then the number is
 rd of 15,
rd of 15, 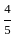 th of 25,
th of 25, 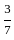 th of 35:
th of 35:
Total number of employees working in a factory was 1800. The number of male and female workers accounted for thrice and twice the number of security staff respectively. 1/5th of female workers, 1/4th of male workers and 1/6th of security staff retired from service on a day. Find the remaining number of employees.
|
23 docs|73 tests
|
|
23 docs|73 tests
|


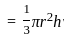
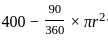
 = 86 sq.cm.
= 86 sq.cm.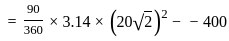 = 228 sq.cm.
= 228 sq.cm.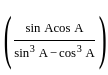
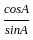 +
+ 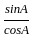 )(sin A - cos A)
)(sin A - cos A)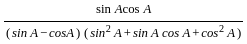
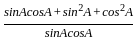 )
)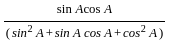
 = ?
= ?
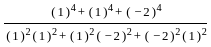
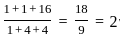
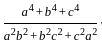
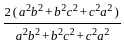 = 2
= 2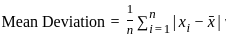
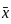 is the mean of the observations,
is the mean of the observations,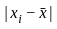 is the absolute deviation of each observation from the mean.
is the absolute deviation of each observation from the mean.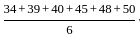 = 42.67
= 42.67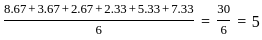
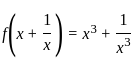 , then f(√3) is equal to
, then f(√3) is equal to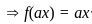
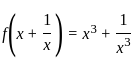

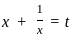
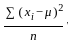
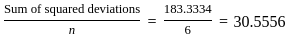

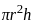
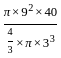 [take height of cyclinder, h = 40 cm]
[take height of cyclinder, h = 40 cm]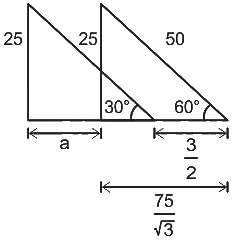
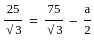
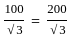 kmph
kmph