Test: Elementary Mathematics - 6 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2024 - Test: Elementary Mathematics - 6
If 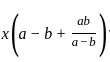 =
= 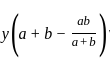 and x + y = 2a3, then what is x-y equal to ?
and x + y = 2a3, then what is x-y equal to ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The circumference of a circle exceeds the diameter by 16.8 cm. What is the diameter of the circle? (Тakе π = 22/7 )
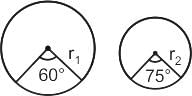
Two equal arcs of different circles C1 and C2 subtend angles of 60° and 75° respectively, at the centres. What is the ratio of the radius of C1 to the radius of C2?
Question: What is the cost of 15 pens, 21 pencils and 18 note books?
Statement-I: The cost of 7 pens, 6 pencils and 5 note books is 200.
Statement-II: The cost of 3 pens, 8 pencils and 7 note books is 210.
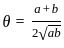 possible?
possible?
Which one of the following is a value of θ, if θ satisfies the equation tan 2θ tan 4θ - 1 = 0; 0 < θ < π/2 ?
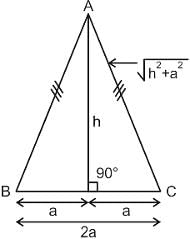
An isosceles triangle has its base length 2a and its height is h. On each side of the triangle a square is drawn external to the triangle. What is the area of the figure thus formed?
If tanx = sin θ + cos θ/sin θ - cos θ , π/4 < θ < π/2 , then what is √2 sin x equal to?
The arch of a bridge is in the form of an arc of a circle. If the span of the bridge is 40 m and height in the middle is 8 m, then what is the radius of curvature of the bridge?
If average weekly wages earned by a worker is Rs. 3,520, then what is the value of k?
How many values of θ will satisfy the equation (sin2 θ - 4 sin θ + 3) (4 - cos2 θ + 4 sin θ) = 0, where 0 < θ < π/2?
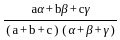 equal to ?
equal to ?
Question: What is the other root of the quadratic equation with real coefficients if one of the roots is 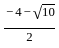 ?
?
Statement-I: The product of the roots is 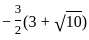
Statement-II: The sum of roots of quadratic equation is -1.
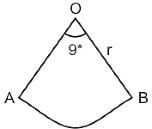
A pendulum swings through an angle of 9° and its end describes an arc of length 14.3 cm. What is the length of the pendulum? (Take π = 22/7)
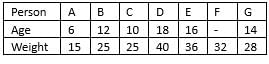
What is the difference between the weights (in kg) of G and C ?
 ; x > 1, then what is the value of x2 - 3x + 2 equal to ?
; x > 1, then what is the value of x2 - 3x + 2 equal to ?
If 2s = a + b + c, then what is s2 + (s - a)(s - b) + (s - b)(s - c) + (s - c)(s - a) equal to ?
A sphere of radius 5 cm is dropped in a right circular cylindrical vessel partly filled with water. The radius of the cylindrical vessel is 10 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel ?
What is the average age (in years) of B, C, D, E and G?
|
23 docs|73 tests
|
|
23 docs|73 tests
|


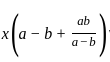 =
=  and x + y = 2a3
and x + y = 2a3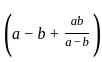 =
= 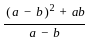
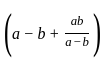 =
= 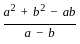
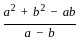 =
= 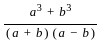
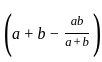 =
= 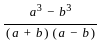
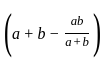 =
= 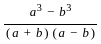

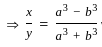
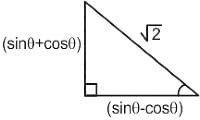
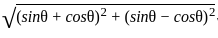
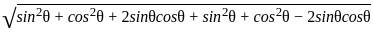
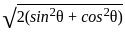 = √2
= √2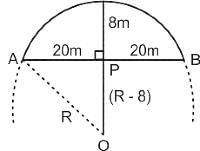
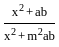 equal to?
equal to?
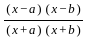 =
= 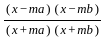
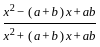 =
= 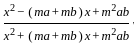
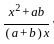 =
= 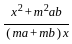
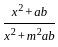 =
= 
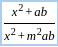 =
= 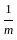
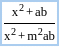 is equal to
is equal to  .
.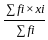
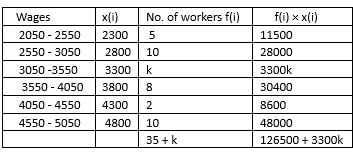
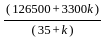
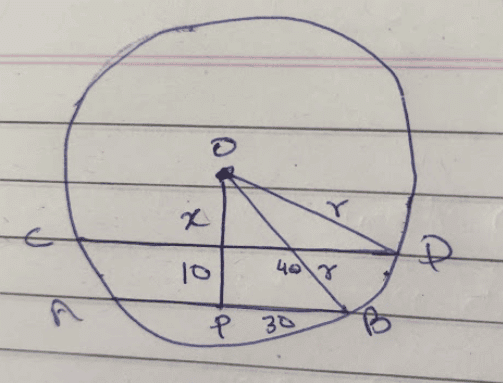
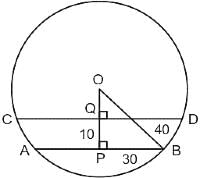
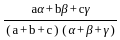 =
= 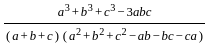
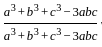 = 1
= 1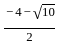
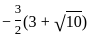
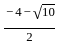
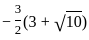
 ×
× 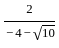

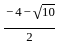 )
)
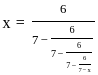
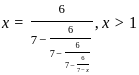

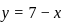 .
.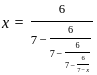
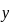 back in,
back in, 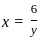 where
where 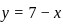
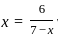
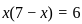
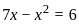
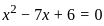
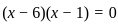
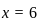 or
or 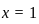 (Since
(Since 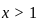 ,
, 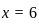 )
) :
: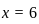 into
into 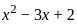 ,
,
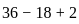
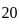
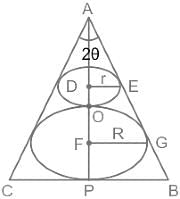
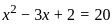 .
.
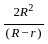
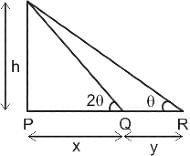

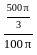 = (500π/3) × (1/100π) = 5/3
= (500π/3) × (1/100π) = 5/3
 =
= 
 .
.















