Test: Elementary Mathematics - 1 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2024 - Test: Elementary Mathematics - 1
Consider the following numbers:
1. 2222
2. 11664
3. 343343
4. 220347
Which of the above are not perfect squares?
2. 11664
3. 343343
4. 220347
For how many integers n, with 10 ≤ n ≤ 100, is n2 + n - 90 divisible by 17?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the following statements:
Statement I: The value of a random variable having the highest frequency is mode.
Statement II: Mode is unique.
Which of the following options is correct in respect of the above statements?
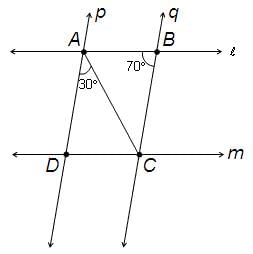
In the figure, if l || m, p || q, ∠DAC = 30° and ∠ABC = 70°, then what is the measure of ∠ACD?
Consider the following statements:
1. If 45°< x < 60°, then sec2x + cosec2x = y2 for some real number y > 1.
2. If 0° < x < 45°, then 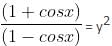 for some real number y > 2.
for some real number y > 2.
3. If 0° < x < 45°, then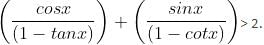
What is the number of true statements?
If θ measured in radians is the angle between the hour hand and the minute hand of a clock when the time is 4:36 pm, then which of the following is correct?
The condition that the roots of the equation px2 + qx + r = 0 are the reciprocals of the roots of equation ax2 + bx + c = 0 is
What is the total number of women visiting parks A and F?
The total population of males of UP, MP and Goa taken together is what percent of the total population of all the given states?
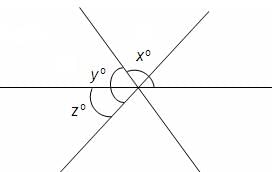
In the figure given below, if x = 120° and y = 100°, then z = ?
An aeroplane flying at a height of 300 m above the ground passes vertically above another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 60° and 45° respectively. What is the height of the lower plane from the ground?
In a 100 m race, A runs at 6 km/hr. If A gives B a start of 8 m and still beats him by 9 seconds, what is the speed of B?
If x = a cosθ + b sinθ and y = a sinθ – b cosθ, then what is x2 + y2 equal to?
The values of a and b for which 3x3 - ax2 - 74x + b is a multiple of x2 + 2x - 24 are:
A car and a bus cover a certain distance in 6 hours and 8(1/2) hours, respectively. What will be the ratio of their speeds if the speed of the car is increased by 50%?
Find the value of x + y, if both x and y are real and x2 + y2 + 2x - 10y = -26.
What is the total surface area of the model of pencil?
A person spends 20% of his income on food, 20% on rent and 30% of the remaining income on shopping and saves the rest. In a particular month, due to the festival season, he spent twice the amount on shopping than what he usually spends. What is the (approximate) percentage decrease in his savings?
If 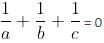 and a + b + c = 5, then find the value of a3 + b3 + c3 - 3abc.
and a + b + c = 5, then find the value of a3 + b3 + c3 - 3abc.
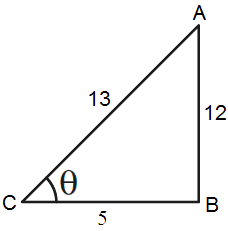
If a triangle has sides 5, 13, and 12 units, and θ is the acute angle of the triangle, then what is the value of (sinθ + cosθ)?
In the figure given below, AB is a diameter of the circle, TD is a tangent to the circle and AB = 2AD. If ∠AHD = 36° and ∠DBA = 30°, then what is the measure of ∠CDT?

A man rows down a river 18 km in 4 hours with the stream, and returns in 10 hours. Consider the following statements:
1. The speed of the man against the stream is 1.8 km/hr.
2. The speed of the man in still water is 3.15 km/hr.
3. The speed of the flow of water in the stream is 1.35 km/hr.
Which of the above statements are correct?
|
23 docs|73 tests
|
|
23 docs|73 tests
|


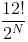 be an odd number?
be an odd number?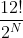 to be an odd number we need to removal all 2's from 12!
to be an odd number we need to removal all 2's from 12!

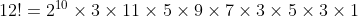
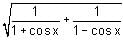 ?
?




 = 60
= 60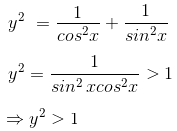
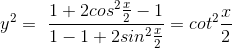
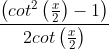

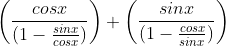
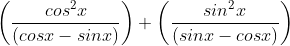

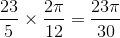
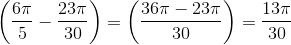
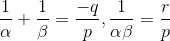
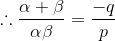
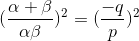
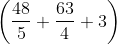 x 100 = (567/20) x 100 = 28.35%.
x 100 = (567/20) x 100 = 28.35%. is not a real number. So, option (4) is not true.
is not a real number. So, option (4) is not true.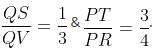

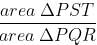 ?
?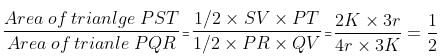


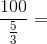 60 seconds
60 seconds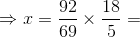 4.8 km/hr
4.8 km/hr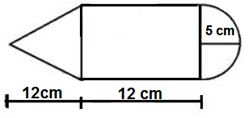
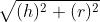
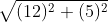

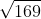 = 13 cm
= 13 cm