CAT Exam > CAT Tests > Logical Reasoning (LR) and Data Interpretation (DI) > Test: Calendars- 1 - CAT MCQ
Test: Calendars- 1 - CAT MCQ
Test Description
10 Questions MCQ Test Logical Reasoning (LR) and Data Interpretation (DI) - Test: Calendars- 1
Test: Calendars- 1 for CAT 2024 is part of Logical Reasoning (LR) and Data Interpretation (DI) preparation. The Test: Calendars- 1 questions and answers have been
prepared according to the CAT exam syllabus.The Test: Calendars- 1 MCQs are made for CAT 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Calendars- 1 below.
Solutions of Test: Calendars- 1 questions in English are available as part of our Logical Reasoning (LR) and Data Interpretation (DI) for CAT & Test: Calendars- 1 solutions in
Hindi for Logical Reasoning (LR) and Data Interpretation (DI) course. Download more important topics, notes, lectures and mock
test series for CAT Exam by signing up for free. Attempt Test: Calendars- 1 | 10 questions in 10 minutes | Mock test for CAT preparation | Free important questions MCQ to study Logical Reasoning (LR) and Data Interpretation (DI) for CAT Exam | Download free PDF with solutions
Test: Calendars- 1 - Question 1
If 15 March 1816 was Friday, what day of the week would 15th April 1916 be?
Detailed Solution for Test: Calendars- 1 - Question 1
Test: Calendars- 1 - Question 2
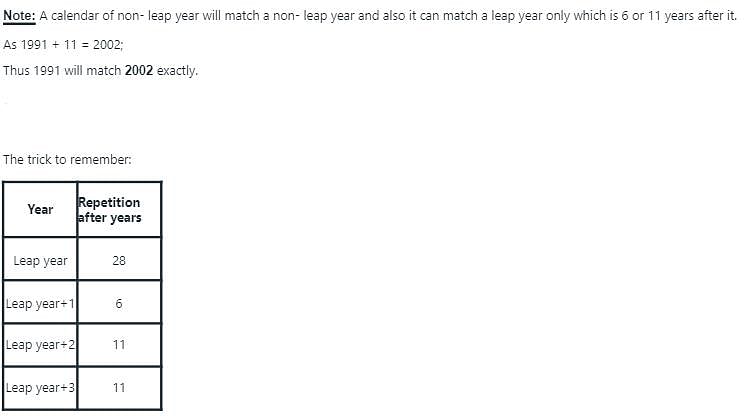
A year 1991 is having a same calendar as that of the year X. Which of the following is a possible valueof X.
Detailed Solution for Test: Calendars- 1 - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Test: Calendars- 1 - Question 3
If 28th August 1946 was a Wednesday, what day of the week was 31 August 1961?
Detailed Solution for Test: Calendars- 1 - Question 3
Test: Calendars- 1 - Question 4
If 09/12/2001(DD/MM/YYYY) happens to be Sunday, then 09/12/1971 would have been a
Detailed Solution for Test: Calendars- 1 - Question 4
Test: Calendars- 1 - Question 5
In 2016, Mohan celebrated his birthday on Friday. Which will be the first year after 2016 when Mohan will celebrate his birthday on a Wednesday? (He was not born in January or February)
Detailed Solution for Test: Calendars- 1 - Question 5
Test: Calendars- 1 - Question 6
If 10th May, 1997 was a Monday, what was the day on Oct 10, 2001?
Detailed Solution for Test: Calendars- 1 - Question 6
Detailed Solution for Test: Calendars- 1 - Question 7
Detailed Solution for Test: Calendars- 1 - Question 8
Detailed Solution for Test: Calendars- 1 - Question 9
Detailed Solution for Test: Calendars- 1 - Question 10
|
88 videos|119 docs|91 tests
|
Information about Test: Calendars- 1 Page
In this test you can find the Exam questions for Test: Calendars- 1 solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Calendars- 1, EduRev gives you an ample number of Online tests for practice
|
88 videos|119 docs|91 tests
|
Download as PDF