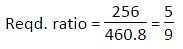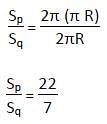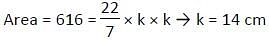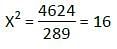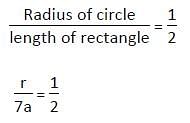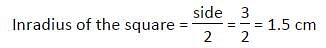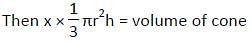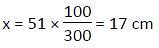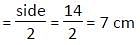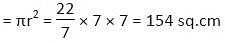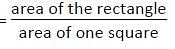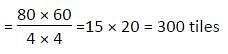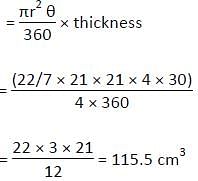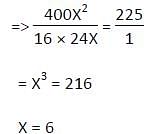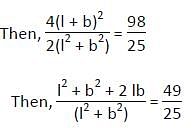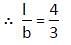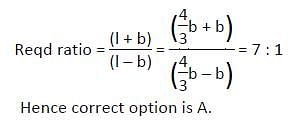MCQ: Area - 1 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Area - 1
If the area of square is 256 cm2 and the breadth of rectangle is 20% more and the length is 50% more than the side of the square, then find the ratio of area of square to the area of rectangle.
P and Q are running on the circumference of two concentric circles, the radius of larger circle is half of the circumference of inner circle. P runs on larger and Q on smaller circle and both complete a round in same time. If both of them run on the larger circle P will beat Q by 75m when they run in the same direction, what is the
circumference of the larger circle?
circumference of the larger circle?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The length of a rectangle, area of which is 126 cm2, is equal to the radius of a circle of area 616 cm2. What is the perimeter of the rectangle?
The shortest distance between two opposite corners of a rectangular park is 68 metres, while the ratio of the length to the breadth of the park is 15 : 8, respectively. Find the difference between the cost of fencing boundary of the park at the rate of Rs. 12/metre and cost of sodding the park at the rate of Rs. 2/metre2.
Perimeter of a rectangle is x cm and circumference of a circle is (x + 8) cm. The length of the rectangle is ______ cm. The ratio of the radius of the circle and the length of the rectangle is 1 : 2 and ratio of length and breadth of the rectangle is 7 : 3.
Some number of solid metallic right circular cones radius of which is equal to the side of the square which area is 9 cm2 and height is 100% more than the inradius of that square are melted to form a solid sphere of radius 6 cm. find the number of right circular cones is required.
The perimeter of a square field is 8cm more than the perimeter of a rectangle. The length of the rectangle is 51 cm which is 300% of its width. If a street of width 10 cm surrounds from outside the square, then find the total cost of constructing the street at the rate of Rs. 25 per sq. cm?
The area of a square is 28 sq. cm more than the area of a rectangle of length 14 cm and breadth 12 cm. What will be the area of incircle of the square?
A rectangular floor of length 80 cm and width 60 cm was fully covered with equal size square tiles of sides 4 cm. If the price of one such tile is Rs. 15 then total how much money will be required to cover the floor with tiles?
The area of a rectangle is one – third of the area of a circle and the length of the rectangle is equal to the diameter of the circle. If the breadth of the rectangle is 11 cm, then what is the perimeter of the rectangle?
The perimeter of two squares fields are 480 cm and 720 cm respectively. The area of a rectangular field is equal to the difference between the areas of these two square fields. The breadth of the rectangular field is 60 cm. How much money the owner of the rectangular field will spend for putting a fence around it at the rate of Rs. 5 per cm?
small slice from a circular shaped pizza of diameter 21 cm and thickness 4 cm was cut. If the small slice makes an angle of 30 degree at the centre of the pizza then what was the total volume (in cm3) of the remaining part of the pizza?
The ratio of length to breadth of a rectangular shaped room is 3 : 4. The length of longest pole that can be placed on the floor of the room is 25 cm. What will be the total cost of cementing the floor of the room at the rate of Rs. 5 per sq. cm?
The breadth of a rectangular field is 80% of its length. Area of square is six times of breadth of the rectangle. If the ratio of Area of Rectangle to Perimeter of Square is 15 : 1, then what will be the length of rectangle ?
‘Jameen’ is a rectangle piece of purposed construction site of a Mohalla ground in Patna. The ratio of the square of the perimeter of ‘Jameen’ and the sum of the squares of the diagonals of ‘Jameen’ is 98 : 25. Find the ratio of the sum of the adjacent sides of ‘Jameen’ and difference of adjacent sides of ‘Jameen’.
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|