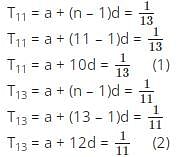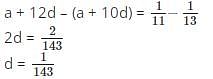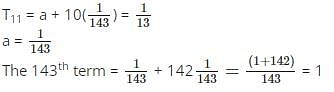MCQ: Arithmetic Progressions - 2 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Arithmetic Progressions - 2
The first four terms of an AP whose a is 10 and d is 10 will be?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the a(2) is 13 and a(5) is 25, then it’s a(7) is
Starting from the last, the 20th term of the A.P. 3, 8, 13, …, 253 is:
What will be the nth term of the AP 1, 5, 9, 13, 17…….?
If the nth term of the AP is 7n – 1, then the first term is ________
What will be the 99th term from the end of the AP 500, 489, 478, 467… – 1139?
If 5 times the 5th term of an AP is equal to 15 times its 15th term, then the value of its 20th term will be _______
If the 7th term of an AP is 20 and its 11th term is 40 then, what will be the common difference?
If the nth term of the AP is 2n + 7, then the common difference will be _____
If the nth term of the AP is 8n + 1, then the 20th term will be ______
If the pth term of an AP is q and its qth term is p, then what will be the value of its (p + q)th term?
What will be the 14th term of the AP 5, 8, 11, 14, 17…….?
If the 11th term of an AP is 1/13 and its 13th term is 1/11, then what will be the value of 143th term?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|