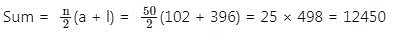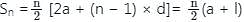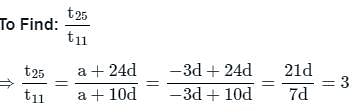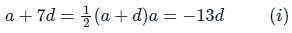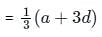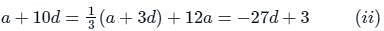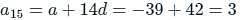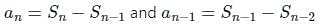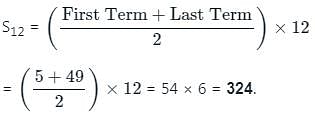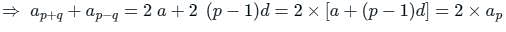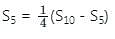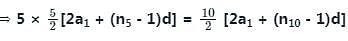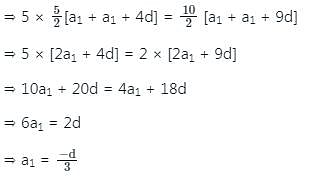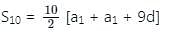MCQ: Arithmetic Progressions - 3 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Arithmetic Progressions - 3
If the 5th term of an A.P. is 31 and 25th term is 140 more than the 5th term. find the A.P.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the sum to n terms of the A.P., whose nth term is 5n + 1
The tenth term common to both the A. P. 3, 7, 11, ... and 1, 6, 11, ... is:
Find the sum of all numbers divisible by 6 in between 100 to 400
If fourth term of an A.P. is zero, then t25/t11 is, where tn denotes the nth
The middle term of arithmatic series 2, 6, 10, ...,146
The eighth term of an A.P. is half of its second term and the eleventh term exceeds one third of its fourth term by 1. Find the 15th term.
The common difference of an A.P., the Sum of whose x terms is Sn, is
If the numbers n - 3, 4n - 2, 5n + 1 are in AP, what is the value of n?
The sum of (p + q)th and (p – q)th terms of an AP is equal to
In an A.P. twenty fifth term is 70 more than to fifteenth term. Find the common differences.
If the first term of an AP is 2 and the sum of the first five terms is equal to one-fourth of the sum of the next five terms, then what is the sum of the first ten terms?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|