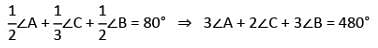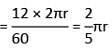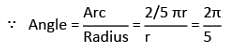MCQ: Complementary angles - 2 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Complementary angles - 2
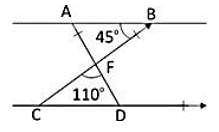
In the given figure, AB || CD, m∠ABF = 45° and m∠CFC = 110°. Then, m∠FDC is:

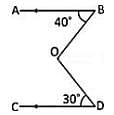
In the given figure, AB || CD, ∠ABO = 40° and ∠CDO = 30°. If ∠DOB = x°, then the value of x is:

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
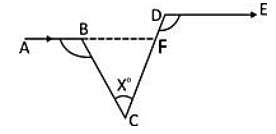
In the adjoining figure, ∠ABC = 100°, ∠EDC = 120° and AB || DE. Then, ∠BCD is equal to:

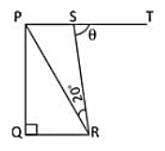
In the trapezium PQRS, QR || PS, ∠Q = 90°, PQ = QR and ∠PRS = 20°. If ∠TSR = θ, then the value of θ is:
In the given figure AB || CD, ∠A = 128°, ∠E = 144°. Then, ∠FCD is equal to:

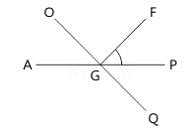
In the given figure lines AP and OQ intersect at G If ∠AGO + ∠PGF = 70° and ∠PGQ = 40°. Find the angle value of ∠PGF.
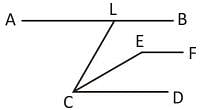
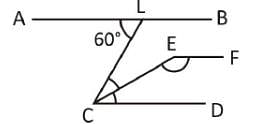
In the given figure AB || CD, ∠ALC = 60° and EC is the bisector of ∠LCD. If EF || AB then the value of ∠CEF is
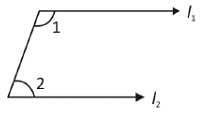
If the arms of one angle are respectively parallel to the arms of another angle, then the two angles are
A wheel makes 12 revolutions per min. The angle in radian described by a spoke of the wheel in 1 s is:
Consider the following statements
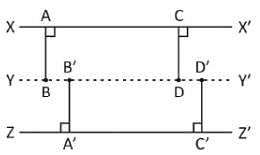
I. The locus of points which are equidistant from two parallel lines is a line parallel to both of them and drawn mid-way between them.
II. The perpendicular distance of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.
Which of the above statements is/are correct?
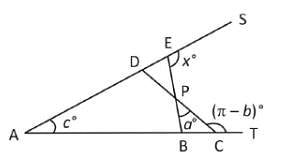
The angles x°, a°, c° and (π – b)° are indicated in the figure given below. Which one of the following is correct?

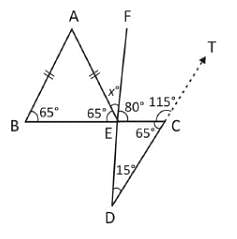
In the figure given below, AB is parallel to CD. ∠ABC = 65°, ∠CDE = 15° and AB = AE. What is the value of ∠AEF?
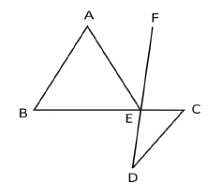
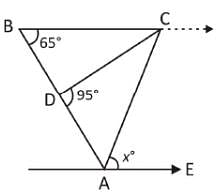
In the figure given below, ABC is a triangle. BC is parallel to AE. If BC = AC, then what is the value of ∠CAE?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|



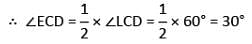
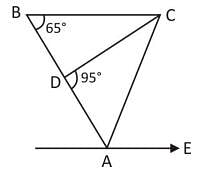
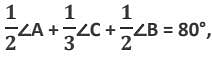 then what is the value of ∠C?
then what is the value of ∠C?