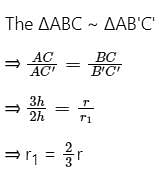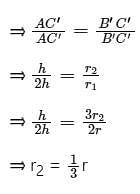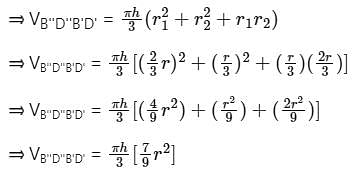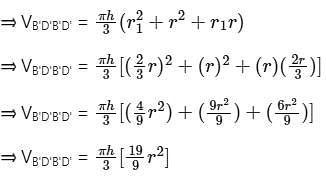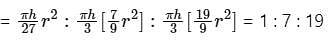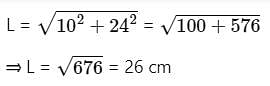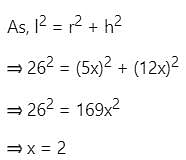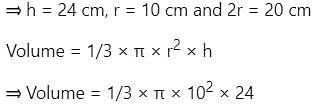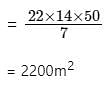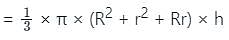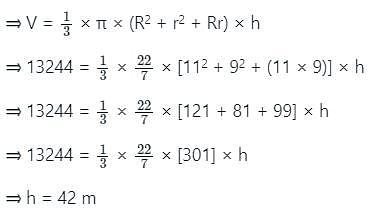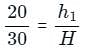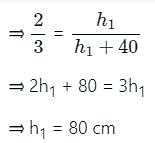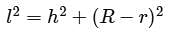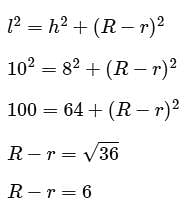MCQ: Cone - 1 - SSC CGL MCQ
10 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Cone - 1
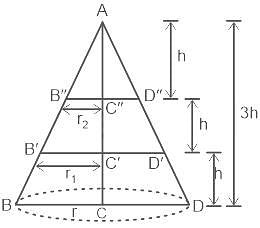
The height of a right circular cone is trisected by two planes parallel to its base at equal distances. The volumes of the three solids, so obtained, starting from the top, are in the ratio:
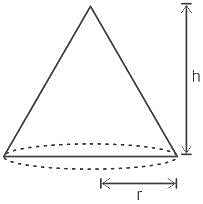
What is the total surface area of a cone whose radius is 10 cm, and height is 24 cm?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
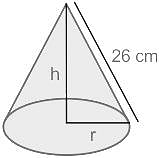
A cone of slant height 26 cm. The height and radius of the cone are in ratio 12:5. Find the height, twice the radius, and volume of the cone.
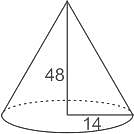
A conical tent of canvas is to be made whose radius of the base is 14 m, and its height is 48 m. How many meters of canvas will be required if the width of the canvas is 8 m?
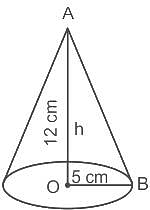
A cone of radius 5 cm and height is 12 cm. Find the ratio of curved surface area to the base area of the cone.
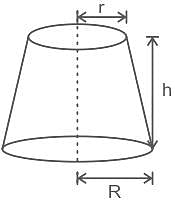
he volume of frustum of a cone is 13244 m3. If the radius of the top circular surface is 9 m and the radius of the other circular surface is 11 m, then find the height of the frustum of a cone. (in m) (Take π = 22/7)
If the curved surface area of a cone is 90% of the total surface area of the cone, then the volume of the cone is how much times the cube of the height of the cone?
A frustum has a top radius of 20 cm and bottom diameter of 60 cm. The height of this frustum is 40 cm. Now, a right circular cone is to be filled over this frustum so that the structure formed is a right circular cone. What should be the height of the cone that is to be filled?
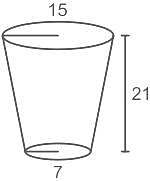
What is the volume of a tumbler having a height of 21 cm and the radii of both circular ends are 15 cm and 7 cm?
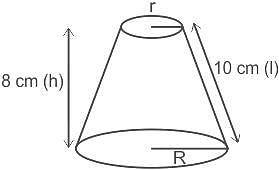
The slant height of a frustum of cone is 10 cm. If the height of the frustum is 8 cm, then find the difference of the radii of its two circular ends?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|