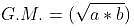MCQ: Geometric Progressions - 1 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Geometric Progressions - 1
A sequence is called ___________________ if an+1 = an * r.
If first term of a G.P. is 20 and common ratio is 4. Find the 5th term.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If r = 1 in a G.P. then what is the sum to n terms?
In G.P. 4, 8, 16, 32, ………… find the sum up to 5th term.
In a G.P., 5th term is 27 and 8th term is 729. Find its 11th term.
How many terms of G.P. 2,4,8,16, …………… are required to give sum 254?
If three positive numbers are inserted between 4 and 512 such that the resulting sequence is a G.P., which of the following is not among the numbers inserted?
The sum of first three terms of a G.P. is 21/2 and their product is 27. Which of the following is not a term of the G.P. if the numbers are positive?
If a sequence is in the form 2*5n then which of the following may be the sequence?
If a = 3 and r = 2 then find the sum up 5th term.
Which term of G.P. 25, 125, 625, …………. is 390625?
Find the sum of series 1+1/2 + 1/4 + ………. up to 6 terms.
The sum of first three terms of a G.P. is 21/2 and their product is 27. Find the common ratio.
Which of the following is the geometric mean of 3 and 12.
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|