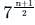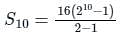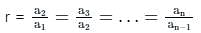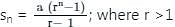MCQ: Geometric Progressions - 2 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Geometric Progressions - 2
If 4th and 5th term of a G.P. are 2 and 8 respectively, then the product of the 1st 8 terms is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
There are four numbers forming a GP in which the third term is greater than the first by 9 and the second term is greater than the fourth by 18. What is the first term?
If the first term is 125 and the common ratio is 2/5, what will be the 4th term of the GP?
If (1/21) + (1/22) + (1/23) .... (1/210) = 1 /k, then what is the value of k?
Find the sum of the series : (20 + 22 + 24 +........+ 28) × 3
After striking the floor, a ball rebounds to 4/5th of the height from which it has fallen. Find the total distance that it travels before coming to rest if it has been gently dropped from a height of 120 meters.
Find the geometric mean of the numbers 7, 72, 73, _________ 7n.
The ratio of 10th term to 7th term of a G.P. is 1 ∶ 8. What is the common ratio of the G.P.?
The third term of a G.P. is 16. The product of its first five terms is:
16, 32, 64, 128,...... The sum of first 10 numbers in the series is:
If G is the G.M. of the product of r sets of observations. With geometric means G1, G2, G3, ……………, Gr respectively, then find the value of G?
The ages of three friends Alpha, Beta and Gamma are in G.P. and the sum of their ages is 57 and the product is 5832. What are their ages?
If the sum of n numbers in the GP 5, 10, 20, ... is 1275 then n is?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|