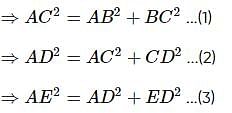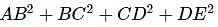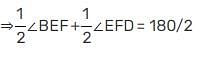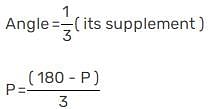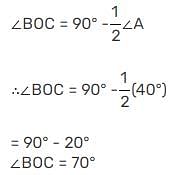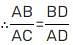MCQ: Geometry - 1 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Geometry - 1
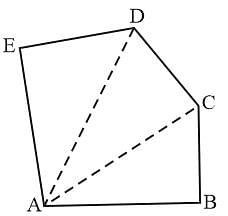
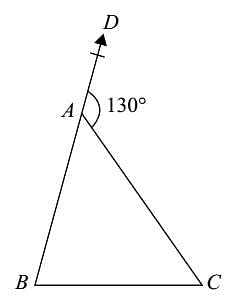
In a polygon ABCDE, BC is perpendicular to AB, CD to AC and DE to AD, then AB2 + BC2 + CD2 + DE2 is
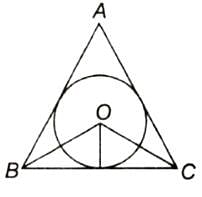
In a triangle ABC, incentre is O and ∠BOC = 110o, then the measure of ∠BAC
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
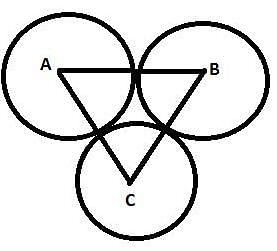
The three equal circles touches each other externally. If the centres of these circles be A, B, C then ΔABC is ________
Two angles are supplementary and the ratio of the angels is 1:4. what is the value of smaller angle?
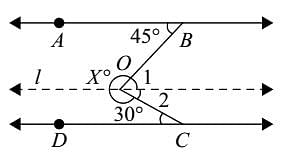
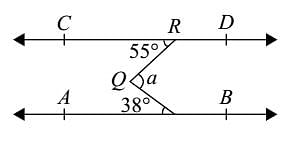
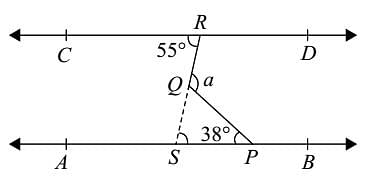
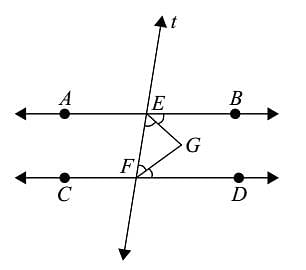
In the adjoining figure, AB || CD, t is the traversal, EG and FG are the bisectors of ∠BEF and ∠DFE respectively, then ∠EGF is equal to:
An angle is equal to one-third of its supplement. Its measure is equal to :
Find the measure of an angle, if six times its complement is 12° less than twice its supplement :
A, B, C are the three angles of a Δ. If A − B = 15° and B − C = 30°. Then ∠A is equal to :
The sides AB and AC of ΔABC have been produced to D and E respectively. The bisectors of ∠CBD and ∠BCE meet at O. If ∠A = 40°, then ∠BOC is equal to:
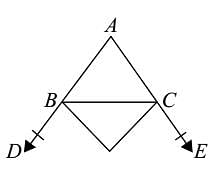
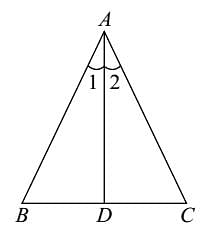
If the bisector of an angle of Δ bisects the opposite side, then the Δ is :
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|