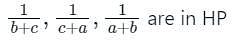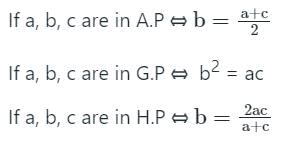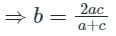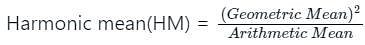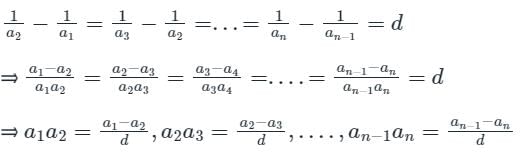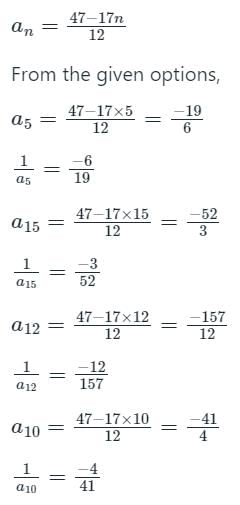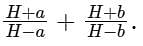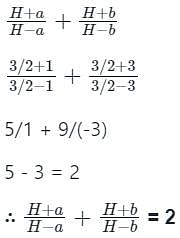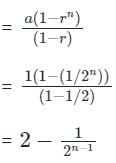MCQ: Harmonic Progressions - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Harmonic Progressions
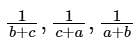 are in HP, then which of the following is/are correct?
are in HP, then which of the following is/are correct?
1. a, b, c are in AP
2. (b + c)2, (c + a)2, (a + b)2 are in GP. Select the correct answer using the code given below.
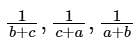 are in HP, then which of the following is/are correct?
are in HP, then which of the following is/are correct?If 1/4, 1/x, 1/10 are in HP, then what is the value of x?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If a, b, c are in geometric progression, then logax x, logbx x and logcx x are in
Three numbers 5, p and 10 are in Harmonic progression if p = ?
The nth terms of the two series 3 + 10 + 17 + ... and 63 + 65 + 67 + .... are equal, then the value of n is:
If xa = yb = zc and x, y and z are in GP, then a, b and c are in
If the roots of the equation a (b - c) x2 + b (c - a) x + c (a - b) = 0 are equal, then which one of the following is correct?
The arithmetic mean and geometric mean of two numbers are 14 and 12 respectively. What is the harmonic mean of the numbers?
If a1, a2, a3, ........ are in H.P., then the expression a1a2 + a2a3 +...... + an - 1 an is equal to:
If the first two terms of a H.P are 2/5 and 12/13 respectively, then the largest term is
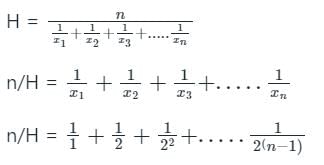
If H is the harmonic mean of numbers 1, 2, 22, 23, ......2n-1 what is n/H equal to?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|


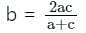 and vice-versa
and vice-versa