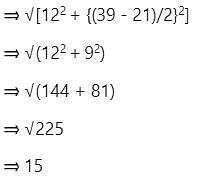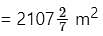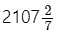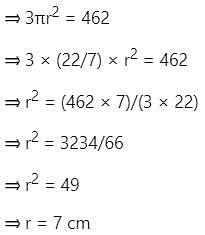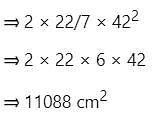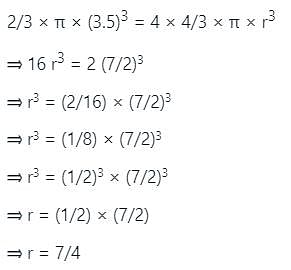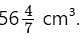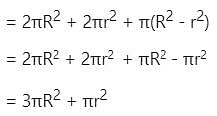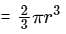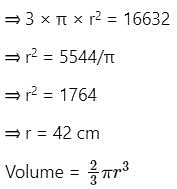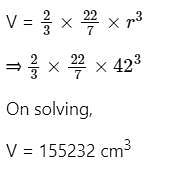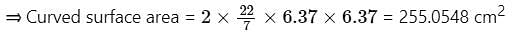MCQ: Hemispheres - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Hemispheres
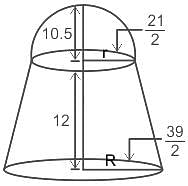
A 22.5 m high tent is in the shape of a frustum of a cone surmounted by a hemisphere. If the diameters of the upper and the lower circular ends of the frustum are 21 m and 39 m, respectively, then find the area of the cloth (in m2) used to make the tent (ignoring the wastage). (Use π = 22/7)
The outer diameter of a rubber ball's cross-section is 22 inches. The rubber has a thickness of 0.5 inches. To the nearest square inch, what is the area of the ball's interior surface? (Use π = 3.14).
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Total surface area of hemisphere is 462 cm2. What is the diameter of hemisphere?
A hemispherical bowl made of iron has inner diameter 84 cm. Find the cost of tin plating it on the inside at the rate of Rs. 21 per 100 cm2 (Use π = 22/7) correct to two places of decimal.
If a solid hemisphere of radius 3.5 cm is converted into four small spheres then find the radius of each small spheres.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height, then the ratio of their volumes is
A solid hemisphere has radius 21 cm. It is melted to form a cylinder such that the ratio of its curved surface area to total surface area is 2 ∶ 5. What is the radius (in cm) of its base (take π = 22/7)
A hemispherical tank full of water is emptied by a pipe at the rate of 7.7 litres per second. How much time (in hours) will it take to empty 2/3 part of the tank, if the internal radius of the tank is 10.5 m?
A hemispherical depression of diameter 4 cm is cut out from each face of a cubical block of sides 10 cm. Find the surface area of the remaining solid (in cm2). (take π = 22/7)
If the diameter of a hemisphere is 28 cm, then what is the volume of hemisphere?
The volume of a solid hemisphere is 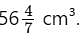 What is its total surface area (in cm²)? (Take π = 22/7)
What is its total surface area (in cm²)? (Take π = 22/7)
The outer and inner radius of a hemispherical bowl are 45 cm and 41 cm, respectively. Find the total surface area of the bowl.
The total surface area of a solid hemisphere is 16632 cm2. Its volume is: (Take π = 22/7)
Steel is used to make a hemispherical bowl that is 0.37 cm thick. The bowl's inner radius is 6 cm. Find the bowl's outside curved surface area (Use π = 22/7)
The radius of large hemisphere is thrice times the radius of small hemisphere. Find the ratio of difference between the volume of large hemisphere and the volume of small hemisphere to the volume of smaller hemisphere?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|