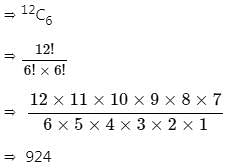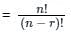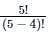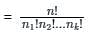MCQ: Permutations and Combinations - 1 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Permutations and Combinations - 1
In how many ways 5 girls and 3 boys be seated in a row, so that no two boys are together?
A volleyball team has 6 people. In how many different ways can teams be made from a class of 12 people?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In how many ways a committee, consisting of 5 men and 6 women can be formed from 8 men and 10 women?
In how many different ways can the letters of the word 'GEOGRAPHY' be arranged such that the vowels must always come together?
From a group of 7 men and 6 women, five persons are to be selected to form a committee so that atleast 3 men are there on the committee. In how many ways can it be done ?
In how many ways can the word CHRISTMAS be arranged so that the letters C and M are never adjacent?
How many four-digit numbers can be formed with digits 2, 5, 6, 7 and 8? (Repeating digits are not allowed)
How many different 6-digit numbers can be formed from the digits 4, 5, 2, 1, 8, 9 ?
If 2nC3 : nC2 = 12 : 1, then the value of n is ?
How many possible two-digit numbers can be formed by using the digits 3, 5 and 7 (repetition of digits is allowed)?
How many 3 digit odd numbers can be formed from the digits 5, 6, 7, 8, 9, if the digits can be repeated
In how many different ways can the letters of the word 'FIGHT' be arranged?
In how many ways can we sort the letters of the word MANAGEMENT so that the comparative position of vowels and consonants remains the same as in MANAGEMENT.
The number of ways of arrangements of 10 persons in four chairs is -
In how many ways can 8 Indians and, 4 American and 4 Englishmen can be seated in a row so that all person of the same nationality sit together?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|