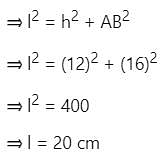MCQ: Regular Right Pyramid with Triangular or Square Base - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Regular Right Pyramid with Triangular or Square Base
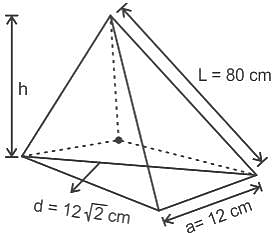
The curved surface area of the right square base pyramid is 1920 cm2. If the diagonal length of the square base is 12√2 cm, then find the (approximate) height of the pyramid. (in cm)
The whole surface area of a pyramid whose base is a regular polygon is 260 cm2 and the area of its base is 120 cm2. The area of each lateral face is 20 cm2. Then the number of lateral faces is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The volume of a pyramid with a square base is 200 cm3. The height of the pyramid is 13 cm. What will be the length of the slant edges (i.e., the distance between the apex and any other vertex), rounded to the nearest integer?
Number of vertices of a triangular pyramid are -
If x, y, and z are the number of faces, edges, and vertices, respectively, of a pentagonal pyramid, then what is the value of 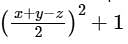 ?
?
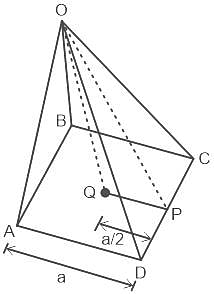
The base of a pyramid is a rectangle whose length and breadth are 16 cm and 12 cm, respectively. If the length of all the lateral edges passing through the vertex of the right rectangular pyramid is 26 cm, then find the volume of the pyramid in cubic centimeter.
The total surface area of a right pyramid, with base as a square of side 8 cm, is 208 cm². What is the slant height (in cm) of the pyramid?
The base of a pyramid is a square of side 10 cm. If its height is 10 cm, then the area (in cm2) of its lateral surface is:
The base of right pyramid is an equilateral triangle, each side of which is 20 cm. Each slant edge is 30 cm. The vertical height (in cm) of the pyramid is:
A square pyramid with side 10 cm has a volume of 400 cm3. Find the total surface area of the pyramid.
The base of a right pyramid is a square and the length of the side of square is 32 cm and height of the pyramid is 12 cm, then what is the total surface area of the square pyramid?
Find the volume of square pyramid, If perimeter of base is 56 cm, and height of pyramid is 12 cm.
The base of a triangular pyramid is an isosceles triangle of sides length are 5 cm, 5 cm and 6 cm. If the height of pyramid is 10 cm then find the volume of the pyramid.
A cylinder of height 28 cm and radius 10 cm is melted and formed into 4 square base pyramids each has the same height H and the base length of each pyramid is equal. Find the height of the pyramid, if the length of its base is 20 cm.
A pyramid has a square base and its slant height is 17 cm and its vertical height is 15 cm. What is the volume of the pyramid?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|


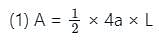
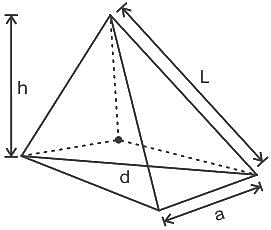
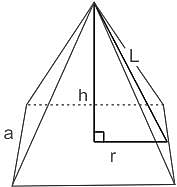
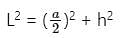
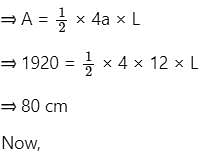
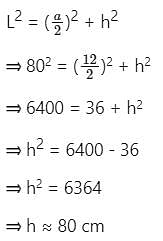

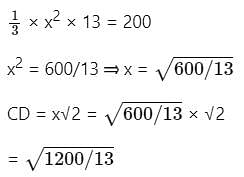
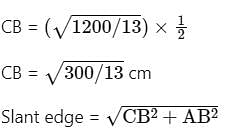
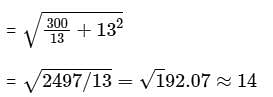

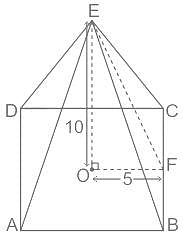
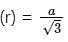
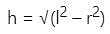
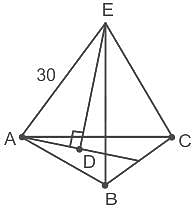
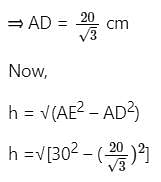
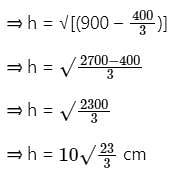
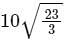 cm.
cm.