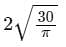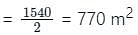MCQ: Right Circular Cylinder - SSC CGL MCQ
10 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Right Circular Cylinder
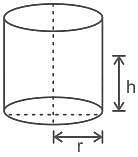
The ratio between the height and radius of the base of a cylinder is 7 ∶ 5. If its volume is 14836.5 cm3, then find its total surface area (take π = 3.14).
The volume of a right circular cylinder is 180 cm3, the area of its base is 30 cm2 and the height is 6 cm then the diameter of the cylinder is (in cm):
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A cylinder has a radius = 7 and height = 30, then find the ratio of the total area of its bases to the total surface area.
Water in a canal 6 m wide and 1.5 m deep is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
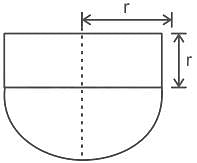
The radius and height of a right circular cylinder are r (in m) and the radius of the hemisphere is also equal to r (in m). A right circular cylinder is surmounted in a solid hemisphere on its base. If the cost of painting is ₹2 per m2 and the total cost of painting the compound object is ₹1540, then find the height of the right circular cylinder. (Take π = 22/7)
The height of a solid cylinder is 35 cm. The circumference of its base is 37 cm more than the radius. What will be the volume of this cylinder ?
The sum of the radius of the base and the height of a solid right circular cylinder is 39 cm. Its total surface area is 1716 cm2. What is the volume (in cm3) of the cylinder? (take π = 22/7)
A solid cylinder has total surface area of 462 sq.cm. If its curved surface area is one-third of its total surface area, then the volume of the cylinder will be
Curved surface area of a cylinder is 308 cm2, and height is 14 cm. What will be the volume of the cylinder?
The radius of a right circular cylinder is 7 cm. Its height is thrice its radius. What is the curved surface area of the cylinder?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|