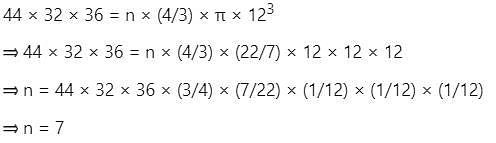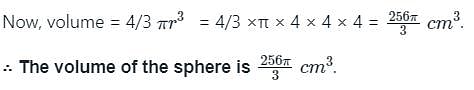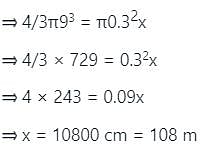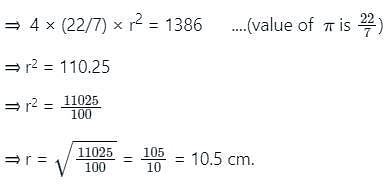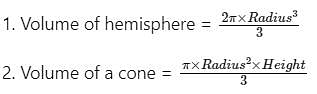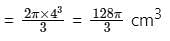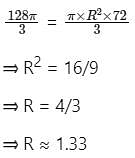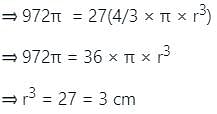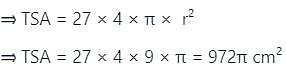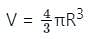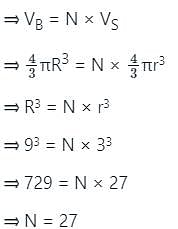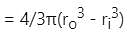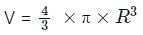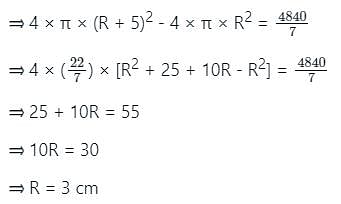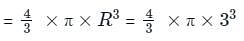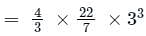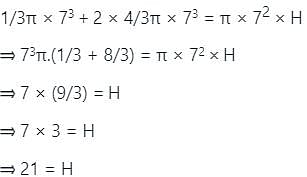MCQ: Sphere - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Sphere
The length of the side of a cube is 5.6 cm. What is the volume of the largest sphere that can be taken out of the cube?
If three solid gold spherical beads of radii 6 cm, 8 cm, and 10 cm, respectively are melted into one spherical bead, then what is the radius (in cm) of the larger bead?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A sphere has a radius of 8 cm. A solid cylinder has a base radius of 4 cm and a height of h cm. If the total surface area of the cylinder is half the surface area of the sphere, then find the height of the cylinder.
A metallic solid cuboid of sides 44 cm, 32 cm and 36 cm melted and converted into some number of spheres of radius 12 cm. How many such sphere can be made with the metal (π = 22/7)?
If the surface area of a sphere is 64 π cm2, then the volume of the sphere is:
A copper sphere of diameter 18 cm is drawn into a wire of diameter 6 mm. Find the length of the wire.
If the surface area of a sphere is 1386 cm2, then find the radius of the sphere.
If the diameter of a sphere is doubled, how does its surface area change?
A hemisphere of lead of radius 4 cm is cast into a right circular cone of height 72 cm. What is the radius of the base of the cone?
The volume of a solid spherical ball was 972πcm3. It was melted and 27 identical spheres were made with the molten material, leaving no wastage. What is the total surface area of the 27 smaller spheres taken together?
A spherical metallic ball S of radius 9 cm. If the bigger metallic spherical ball S is melted and recast into N number of smaller spherical balls of radius 3 cm, then find the value of N.
A hollow sphere has an outer radius of 4 cm and inner radius of 1 cm. What is the volume of this hollow sphere?
0.1 per cent of 1.728 x 106 spherical droplets of water, each of diameter 2 mm, coalesce to form a spherical bubble. What is the diameter (in cm) of the bubble?
When the radius of a sphere is increased by 5 cm, its surface area increases by 4840/7 cm2. What is the volume (in cm3) of the original sphere? (Take π = 22/7, nearest to an integer)
A solid cone of radius 7 cm and height 7 cm was melted along with two solid spheres of radius 7 cm each to form a solid cylinder of radius 7 cm. What is the curved surface area (in cm2) of the cylinder? (Use π = 22/7)
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|