MCQ: Height & Distance - 2 - SSC CGL MCQ
15 Questions MCQ Test SSC CGL Tier 2 - Study Material, Online Tests, Previous Year - MCQ: Height & Distance - 2
A man on the top of a vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 10 minutes for the angle of depression to change from 45° to 60°, how soon after this will the car reach the observation tower?
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
From The highest point of a 10 m high building, the edge of rise of the of the highest point of a tower is 60° and the despondency's edge of its foot is 45°, Find The tower's stature. (take√3 = 1.732)
A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60º. What is the distance between the base of the tower and the point P?
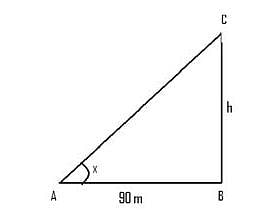
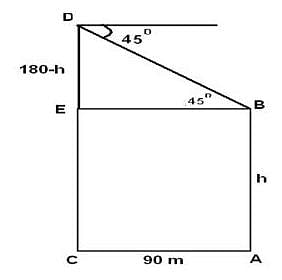
The horizontal distance between two towers is 90 m. The angular depression of the top of the first as seen from the top of the second which is 180 m high is 450. Then the height of the first is
The angle of elevation of the sun, when the length of the shadow of a tree √3 times the height of the tree, is:
A man is watching form the top of the tower a boat speeding away from the tower. The boat makes the angle of depression of 60° with the man's eye when at a distance of 75 meters from the tower. After 10 seconds the angle of depression becomes 45°. What is the approximate speed of the boat, assuming that it is running in still water?
From a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 100 m high, the distance of point P from the foot of the tower is:
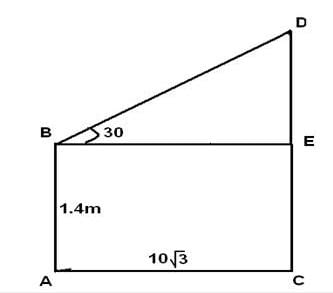
An observer 1.4 m tall is 10√3 away from a tower. The angle of elevation from his eye to the top of the tower is 60°. The heights of the tower is
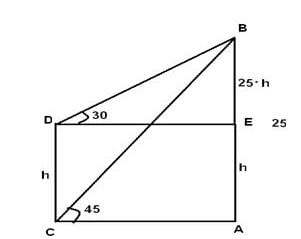
The Top of a 25 meter high tower makes an angle of elevation of 450 with the bottom of an electric pole and angle of elevation of 30 degree with the top of pole. Find the height of the electric pole.
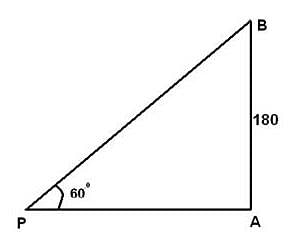
From a point P on a level ground, the angle of elevation of the top tower is 60°. If the tower is 180 m high, the distance of point P from the foot of the tower is
The heights of two towers are 90 meters and 45 meters. The line joining their tops make an angle 450 with the horizontal then the distance between the two towers is
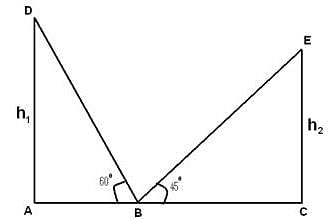
The angles of elevation of the tops of two vertical towers as seen from the middle point of the lines joining the foot of the towers are 45° & 60°.The ratio of the height of the towers is
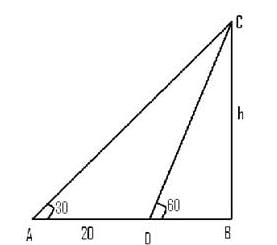
On the level ground, the angle of elevation of the top of a tower is 30°.on moving 20 meters nearer, the angle of elevation is 60°. Then the height of the tower is
The angle of elevation of a tower at a point 90 m from it is cot-1(4/5). Then the height of the tower is
|
1365 videos|1312 docs|1010 tests
|
|
1365 videos|1312 docs|1010 tests
|


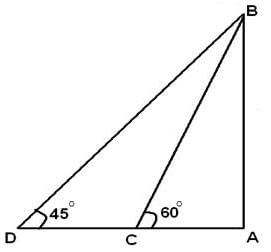
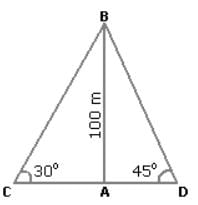
 ACB = 30° and
ACB = 30° and  ADB = 45°.
ADB = 45°.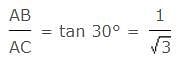
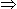
 CD = (AC + AD)= (1003 + 100) m
CD = (AC + AD)= (1003 + 100) m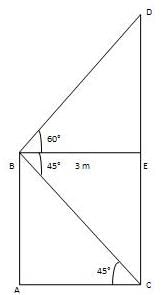

 ACB = θ.
ACB = θ.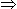 cot
cot 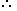 θ = 30º.
θ = 30º.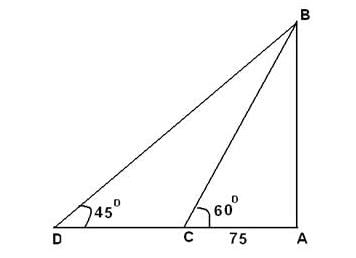
 APB = 30º and AB = 100 m.
APB = 30º and AB = 100 m.
 AP= (AB x √3) m
AP= (AB x √3) m