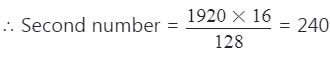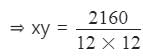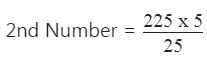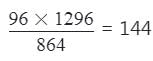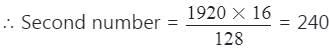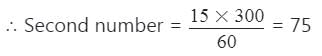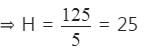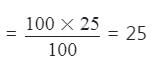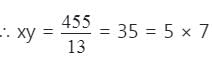MCQ: HCF & LCM - 1 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: HCF & LCM - 1
The LCM of two numbers is 1920 and their HCF is 16. If one of the number is 128, find the other number.
The HCF of two numbers is 15 and their LCM is 225. If one of the number is 75, then the other number is ?
The L.C.M. of three different numbers is 120. Which of the following cannot be their H.C.F.?
The product of two numbers is 1280 and their H.C.F. is 8. The L.C.M. of the number will be ?
The HCF and LCM of two numbers are 12 and 924 respectively. Then the number of such pairs is
The product of two numbers is 2160 and their HCF is 12. Number of such possible pairs is
LCM of two numbers is 225 and their HCF is 5. If one number is 25, the other number will be?
The HCF of two numbers is 23 and the other two factors of their LCM are 13 and 14. The larger of the two numbers is :
The H.C.F. of two numbers is 96 and their L.C.M. is 1296. If one of the number is 864, the other is
The LCM of two numbers is 1920 and their HCF is 16. If one of the number is 128, find the other number.
The HCF of two numbers is 15 and their LCM is 300. If one of the number is 60, the other is :
The LCM of two numbers is 4 times their HCF. The sum of LCM and HCF is 125. If one of the number is 100, then the other number is
The HCF of two numbers is 23 and the other two factors of their LCM are 13 and 14. The larger of the two numbers is :
The HCF and LCM of two numbers are 13 and 455 respectively. If one of the number lies between 75 and 125, then, that number is :
The LCM of two numbers is 864 and their HCF is 144. If one of the number is 288, the other number is :
|
344 videos|316 docs|185 tests
|