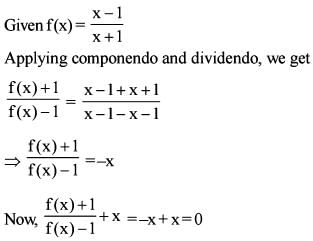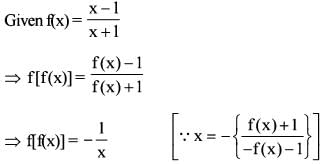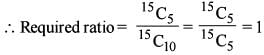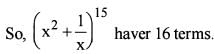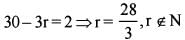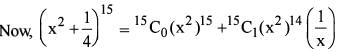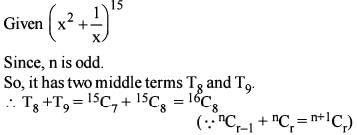NDA I - Mathematics Question Paper 2014 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Past Year Papers - NDA I - Mathematics Question Paper 2014
Every quadratic equation ax2 +bx+c= 0 where a,b,c Every quadratic equation ax2 +bx+c= 0 where a,b,c 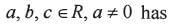
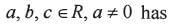
The relation S is defined on the set of integers Z as xSy if integer x devides integer y. Then
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If 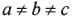 are all positive, then the value of the
are all positive, then the value of the
determinant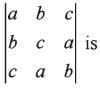
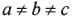 are all positive, then the value of the
are all positive, then the value of thedeterminant
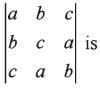
Which of the following statements are correct ?
1. A2 = A
2.B2 = B
3 .(AB)2=AB
Q. Select the correct answer using the code given below:
Let z be a complex number such that |z| = 4 and arg z =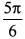
Q. Where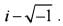 What is z equal to ?
What is z equal to ?
If 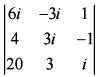 x + iy, where
x + iy, where 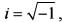 then what is x equal to ?
then what is x equal to ?
If 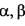 are the roots of ax2 +bx + c =
are the roots of ax2 +bx + c = 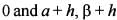 are the roots of px2 +qx + r = 0, then what is h equal to ?
are the roots of px2 +qx + r = 0, then what is h equal to ?
If the matrix A is such that 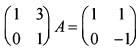 then what is A equal to ?
then what is A equal to ?
Consider the following statements :
1. Determinant is a square matrix.
2. Determinant is a number associated with a square
Q. Which of the above statements is/are correct ?
If A is an invertible matrix, then what is det (A~l) equal to ?
From the matrix equation AB=AC, Where A, B, C are the square matrices of same order, we can conclude B = C provided
If A = 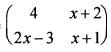 is symmetric, th en w hat is x equal to ?
is symmetric, th en w hat is x equal to ?
If 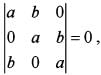 then which one o f the following is correct ?
then which one o f the following is correct ?
The function f : N → N , N being the set o f o f natural numbers, defined by f( x) = 2x + 3 is
What is 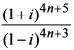 equal to, where n is a natural number and
equal to, where n is a natural number and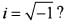
What is the number of ways in which one can post 5 letters in 7 letters boxes ?
What is the number of ways that a cricket team of 11 players can be made out of 15 players ?
A and B are two sets having 3 elements in common. Ifn(A) = 5, n(B) = 4, then what is n(A x B) equal to ?
If f (x) = a x + b and g(x) = cx+d such that f [g(x)] = g [f(x)] then which one of the following is correct?
If A and B are square matrices of second order such that | A | = - l , |B| = 3, then w hat is |3AB| equal to ?
Consider the function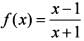
Consider the expansion 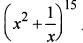
Q. What is the independent term in the given expansion ?
What is the ratio of coefficient o f x15 to the term independent of x in the given expansion ?
Consider the following statements:
1. There are 15 terms in the given expansion.
2. The coefficient o f x 12 is equal to the at of x3.
Q. Which of the above statements is/are correct ?
Consider the following statements:
1. The term containing x2 does not exist in the given expansion.
2. The sum of the coefficients of all the terms in the given expansion is 215.
Q. Which of the above statements is/are correct ?
What is the sum of the coefficients of the middle terms in the given expansion ?
|
71 docs|22 tests
|
|
71 docs|22 tests
|





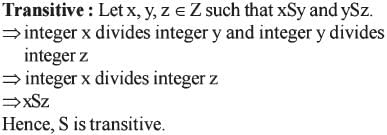
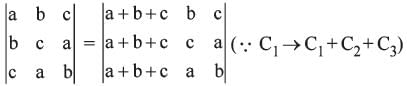
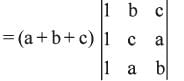
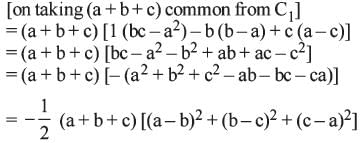


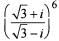 equal to, where
equal to, where 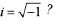
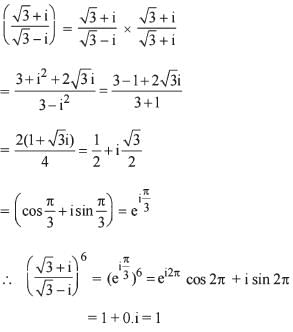
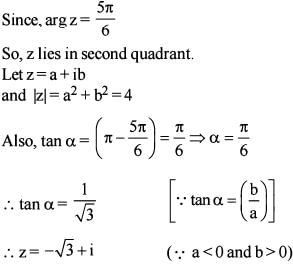
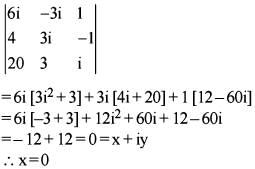

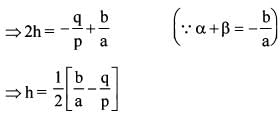
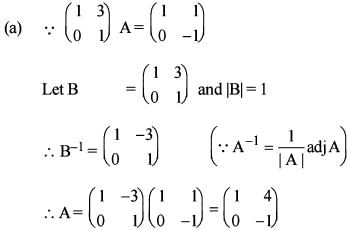
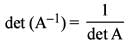
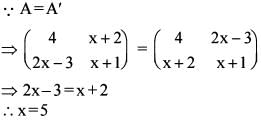
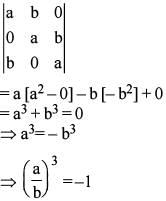

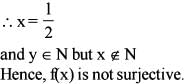
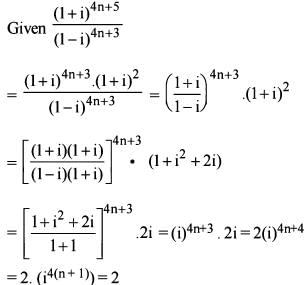
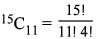

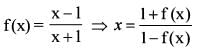
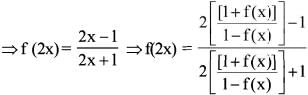
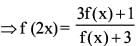
 is equal to ?
is equal to ?