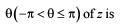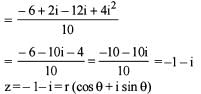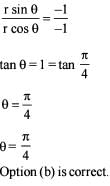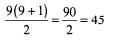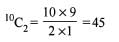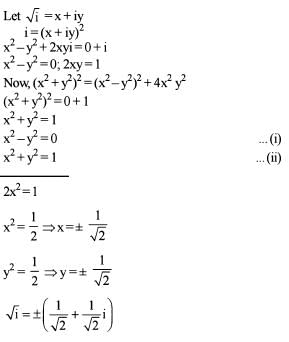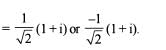NDA I - Mathematics Question Paper 2015 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Past Year Papers - NDA I - Mathematics Question Paper 2015
Let θ be a positive angle. If the number of degrees in θ is divided by the number of radians in θ, then an irrational number 180/π results. If the number of degrees in θ is71multiplied by the number of radians in θ, then an irrational number 125π/9 results. The angle θ must be equal to
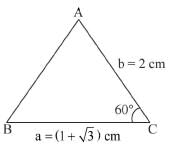
In a triangle ABC, a = (1 + a/3) cm, b = 2 cm and angle C = 60°.Then the other two angles are
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let α be the root of the equation 25cos2θ+ 5cosθ - 12 = 0 where 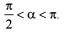
Q. What is tan α equal to?
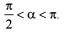
Let a be the root of the equation 25cos2θ + 5cosθ - 12 = 0,where 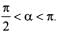
Q. What is sin 2 α equal to?
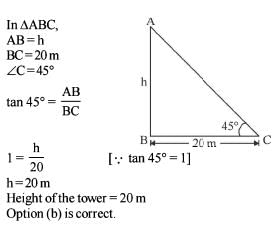
The angle of elevation of the top of a tower from a point 20 m away from its base is 45°. What is the height of the tower?
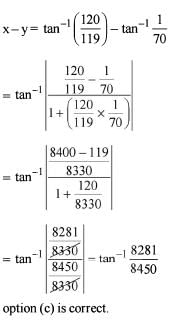
The equation tan-1 (1 +x) + tan-1 (1-x) = π/2 is satisfied by
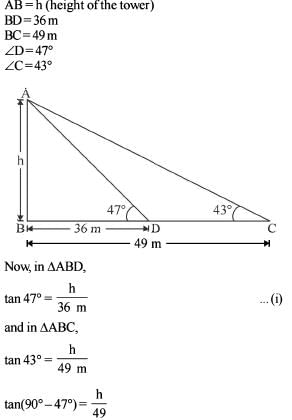
The angles of elevation of the top of a tower standing on a horizontal plane from two points on a line passing through the foot of the tower at distances 49 m and 36 m are 43° and 47° respectively. What is the height of the tower?
Consider the triangle ABC with vertices A (-2,3), B (2,1) and C (0,2)
Q. What is the circumcentre of the triangle ABC?
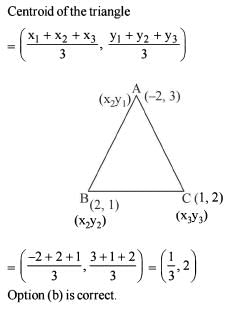
Consider the triangle ABC with vertices A (-2,3), B (2,1) and C (0,2).
Q. What is the centroid of the tirnalge ABC?
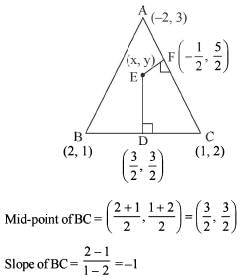
Consider the triangle ABC with vertices A (-2,3), B (2,1) and C (0,2).
Q. What is the foot of the altitude from the vertex A of the triangle ABC?
Let X be the set of all persons living in a city. Persons x,y in X are said to be related as x < y ify is at least 5 years older than x. Which one of the following is correct?
Which one of the following matrices is an elementary matrix?
Consider the following statements in respect of the given equation:
(x2 + 2)2 + 8x2 = 6x(x2 + 2)
1. All the roots of the equation are complex.
2. The sum of all the roots of the equation is 6.
Q. Which of the above statements is/are correct?
In solving a problem that reduces to a quadratic equation, one student makes a mistake in the constant term and obtains 8 and 2 for roots. Another student makes a mistake only in the coefficient of first-degree term and finds -9 and-1 for roots. The correct equation is
In a class of 60 students, 45 students like music, 50 students like dancing, 5 students like neither. Then the number of students in the class who like both music and dancing is
If log10 2, log10 (2x- 1) and log10(2x+ 3 ) are three consecutive terms of an A.P, then the value of x is
Let Z be the set of integers and aRb, where a, b ∈ Z if and only if (a - b) is divisible by 5.
Consider the following statements:
1. The relation R partitions Z into five equivalent classes.
2. Any two equivalent classes are either equal or disjoint.
Q. Which of the above statements is/are correct?
If m and n are the roots of the equation (x+p)(x + q)=0, then the roots of the equation (x - m) (x - n) + k = 0 are
If 1, ω, ω2 are the cube roots of unity, then the value of(l + ω)(l + ω2)(l + ω4)(l + ω8) is
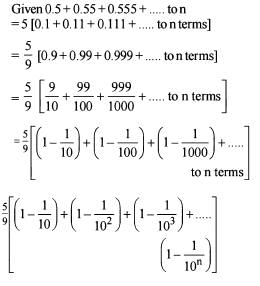
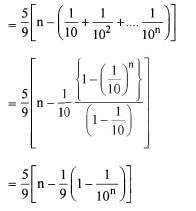
What is the sum of the series 0.5 + 0.55 + 0.555 + ... to n terms?
Let A = { 1,2,3,4,5,6,7,8,9,10}. Then the number of subsets of A containing exactly two elements is
What is the square root of i, where i =√-1?
|
71 docs|22 tests
|
|
71 docs|22 tests
|





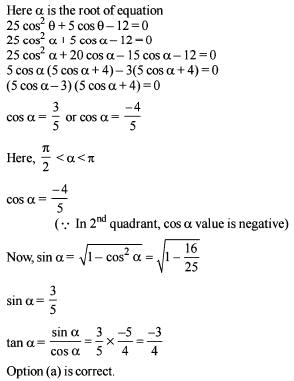

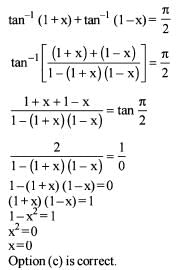


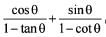 equal to?
equal to?
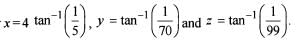

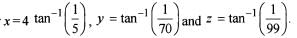








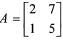 then that is A + 3A-1 equal to?
then that is A + 3A-1 equal to?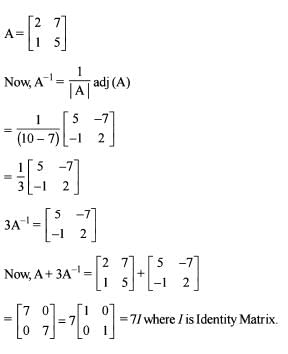

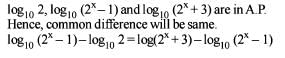
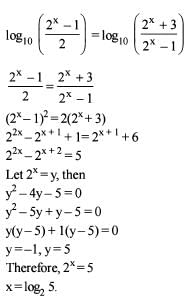
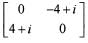 is
is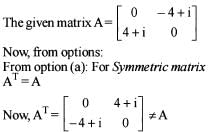
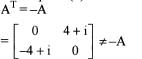
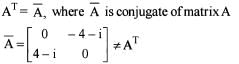

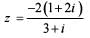 where
where 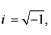 then argument
then argument