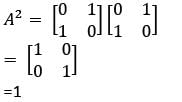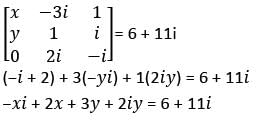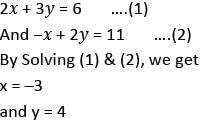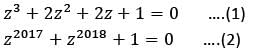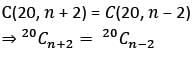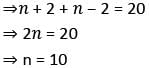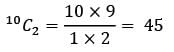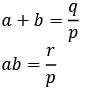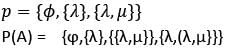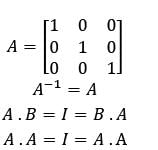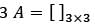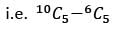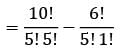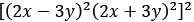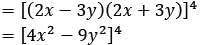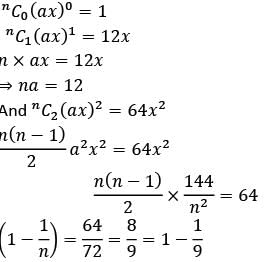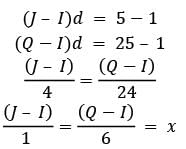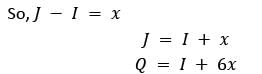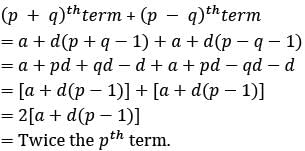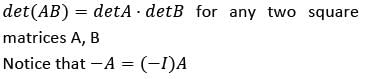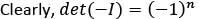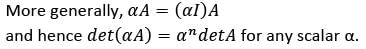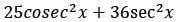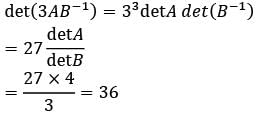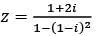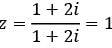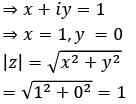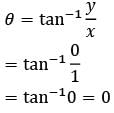NDA I - Mathematics Question Paper 2019 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Past Year Papers - NDA I - Mathematics Question Paper 2019
What is the nth term of the sequence 25, -125, 625, -3125, ...?
Suppose X = {1, 2, 3, 4} and R is a relation on X. If R = [(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (3, 2)}, then which one of the following is correct?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A relation R is defined on the set N of natural numbers as xRy ⇒ x2 − 4xy + 3y2 = 0. Then which one of the following is correct?
If A= (x ∈ Z∶ x3 − 1 = 0) and B = (x ∈ Z ∶ x2 + x + 1 = 0), where Z is set of complex numbers, then what is A ∩ B equal to?
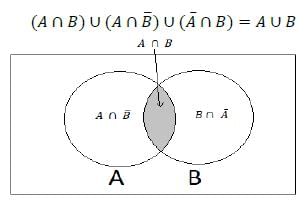
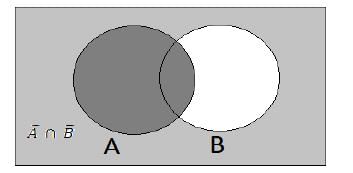
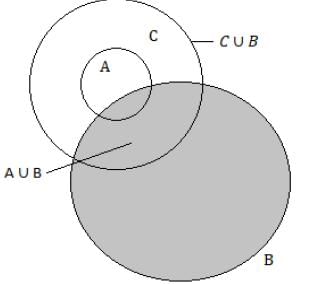
Consider the following statements for the two non-empty sets A and B:
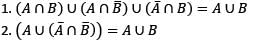
Q. Which of the above statements is/are correct?
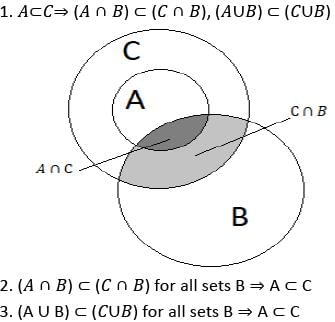
Let X be a non-empty set and let A, B, C be subsets of X. Consider the following statements:
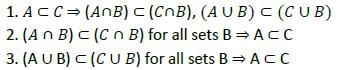
Q. Which of the above statements are correct?
What are the roots of the equation | x2 - x - 6 | = x + 2?
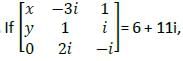 then what are the values of x and y respectively?
then what are the values of x and y respectively?
The common roots of the equations z3 + 2z2 + 2z + 1 = 0 and z2017 + z2018 + 1 = 0 are
If C(20, n + 2) = C(20, n − 2), then what is n equal to?
There are 10 points in a plane. No three of these points are in a straight line. What is the total number of straight lines which can be formed by joining the points?
The equation px2 + qx + r = 0 (where p, q, r, all are positive) has distinct real roots a and b. Which one of the following is correct?
If A = {λ,{λ,μ}}, then the power set of A is
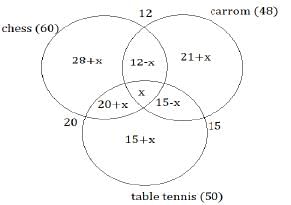
In a school, all the students play at least one of three indoor games – chess, carrom and table tennis. 60 play chess, 50 play table tennis, 48 play carrom, 12 play chess and carrom, 15 play carrom and table tennis, 20 play table tennis and chess.
Q. What can be the minimum number of students in the school?
In a school, all the students play at least one of three indoor games – chess, carrom and table tennis. 60 play chess, 50 play table tennis, 48 play carrom, 12 play chess and carrom, 15 play carrom and table tennis, 20 play table tennis and chess.
Q. What can be the maximum number of students in the school?
If A is an identity matrix of order 3, then its inverse (A−1)
A is a square matrix of order 3 such that its determinant is 4. What is the determinant of its transpose?
From 6 programmers and 4 typists, an office wants to recruit 5 people. What is the number of ways this can be done so as to recruit at least one typist?
What is the number of terms in the expansion of [(2x - 3y)2 (2x + 3y)2]2?
In the expansion of (1 + ax)n , the first three terms are respectively 1, 12x and 64x2 . What is n equal to?
The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) of
The sum of (p+q)th and (p-q)th terms of an AP is equal to
If A is a square matrix of order n > 1, then which one of the following is correct?
What is the least value 25 cosec2 x + 36 sec2 x?
Let A and B be (3×3) matrices with det A = 4 and det B = 3
Q. What is det (2AB) equal to?
Let A and B be (3×3) matrices with det A = 4 and det B = 3
Q. What is det (3AB−1) equal to?
A complex number is given by 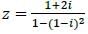
Q. What is the modulus of z?
A complex number is given by 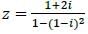
What is the principal argument of z?
|
71 docs|22 tests
|
|
71 docs|22 tests
|


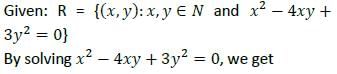
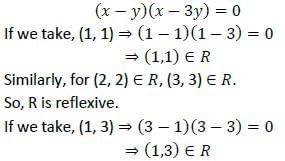
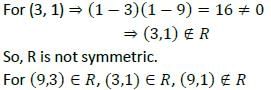
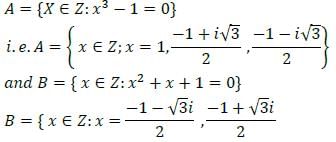
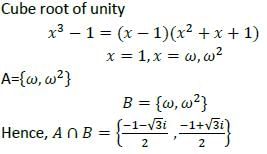

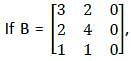 then what is adjoint of B equal to?
then what is adjoint of B equal to?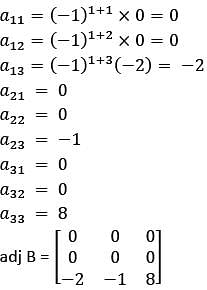
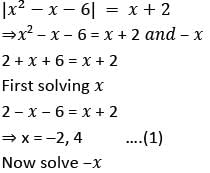
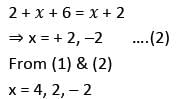
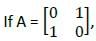 then the matrix A is a/an
then the matrix A is a/an