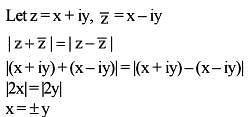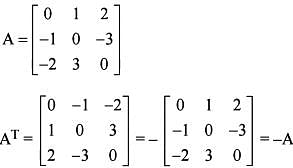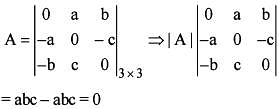NDA II - Mathematics Question Paper 2014 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Past Year Papers - NDA II - Mathematics Question Paper 2014
Let X be the set of all citizens of India. Elements x, y in X aresaid to be related if the difference of their age is 5 years. Which one of the following is correct ?
2. Consider the following relations from A to B where A = {u, v, w, x, y, z} and B= {p,q, r, 5}.
1. {(u,p), (y,p), (w,p), (x, q), (y, q), (z, q)}
2. {(u,p),(y,q),(w,r),(z,s)}
3. {(«, s), (v, r), (w, q), (u,p), (v, q), (z, q),}
4. {(u, q), (v,p), (w, s), (x, r), (y, q), (z, $),}
Which of the above relations are not functions ?
1. {(u,p), (y,p), (w,p), (x, q), (y, q), (z, q)}
2. {(u,p),(y,q),(w,r),(z,s)}
3. {(«, s), (v, r), (w, q), (u,p), (v, q), (z, q),}
4. {(u, q), (v,p), (w, s), (x, r), (y, q), (z, $),}
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If a and P are the roots of the equation ax2 + bx + c = 0, where a  0, then (aα + b){aβ+ b) is equal to:
0, then (aα + b){aβ+ b) is equal to:
 0, then (aα + b){aβ+ b) is equal to:
0, then (aα + b){aβ+ b) is equal to:Let S denote set of all integers. Define a relation R on S as 'aRb if ab ≥ 0 where a, b ∈ S. Then R is :
The roots of the equation a2x2 - 2 abx + b2 = 0 when a < 0 and b > 0 are:
What is the sum of the two numbers (11110)2 and (1010)2 ?
Let N denote the set of all non-negative integers and Z denote the set of all integers. The function Z → N given by  is:
is:
If P and Q are two complex numbers, then the modulus of the quotient of P and Q is :
Let z = x + iy Where x, y are real variables i = √-i. If |2z -1| = |z - 2|, then the point z describes :
The sum of an infinite GP is x and the common ratio r is such that |r| < 1. If the first term of the GP is 2, then which one of the following is correct ?
A box contains 3 white and 2 black balls. Two balls aredrawn at random one after the other. If the balls are not replaced, what is the probability that both the balls are black?
For two variables x and y, the two regression coefficients are byx = -3/2 and bxy = - 1/6. The correlation coefficient between x and y is :
The variance of numbers x1,x2,x3,.......xn, is V Consider the following statements :
1. If every xi is increased by 2, the variance of the new set of the new set of numbers is V.
2. If the numbers xi is squared, the variance of the new set is V2.
Which of the following statements is/are correct ?
What is the mean of the squares of the first 20 natural numbers ?
p, q, r, s, t, are five numbers such that the average ofp,q and r is 5 and that of s and t is 10. What is the average of all the five numbers ?
The cumulative frequency of the largest observed value must always be:
It has been found that if A and B play a game 12 times, A wins 6 times, B wins 4 times and they draw twice. A and B take part in a series of 3 games. The probability that they win alternately, is :
Out of 7 consonants and 4 vowels, words are to be formed by involving 3 consonants and 2 vowels. The number of such words formed is :
Let X denote the number of scores which exceed 4 in 18, tosses of a symmetrical die. Consider the following statements:
1. The arithmetic mean o f X is 6.
2. The standard deviation ofX is 2.
Which of the above statements is/are correct ?
How many different words can be formed by taking four letters out of the letters of the word 'AGAIN' if each word has to start with A ?
The sum of the series formed by the sequence 3, √3, 1. upto infinity i s :
The number 251 in decimal system is expressed in binary system by :
What is the argum ent o f the complex number
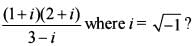
Consider the following statements in respect of the matrix

1. The matrix A is skew-symmetric.
2. The matrix A is symmetric.
3. The matrix A is invertible.
Which of the above statements is/are correct ?
Consider two matrices 
Which one of the following is correct ?
If A is any matrix, then the product AA is defined only when A is a matrix o f order m x n where :
The determinant of an odd order skew symmetric matrix is always:
If any two adjacent rows or columns of a determinant are intercharged in position, the value of the determinant:
|
71 docs|22 tests
|
|
71 docs|22 tests
|



 (R is not reflexive)
(R is not reflexive)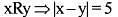
 (R is symmetric)
(R is symmetric)
 (R is not transitive)
(R is not transitive)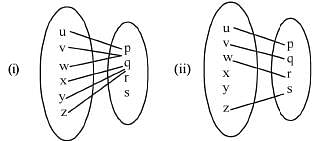

 0) α and β are roots of given equation.
0) α and β are roots of given equation.
 a, b ∈ S
a, b ∈ S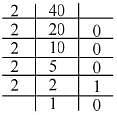


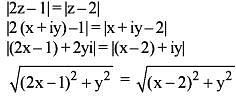
 x(where, a = 1st term and r = common ratio)
x(where, a = 1st term and r = common ratio)
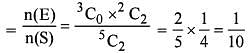


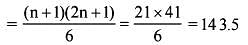
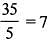



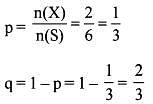



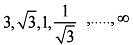
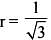

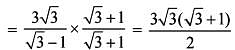
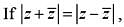 then the locus o f z is:
then the locus o f z is: