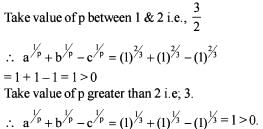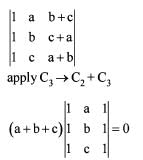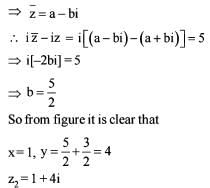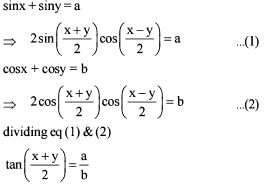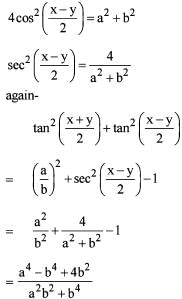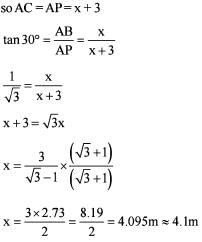NDA II - Mathematics Question Paper 2015 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Past Year Papers - NDA II - Mathematics Question Paper 2015
Let X be the set of all persons living in Delhi. The persons a and b in X are said to be related if the difference in their ages is at most 5 years. The relation is
The matrix A= 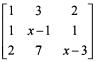 will have inverse for every real number x except for
will have inverse for every real number x except for
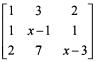 will have inverse for every real number x except for
will have inverse for every real number x except for| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the value of the determinant is positive, where a ≠ b ≠ c, then the value of abc
Consider the following statements in respect of the determinant
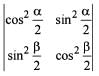
where α, β are complementary angles
1. The value of the determinant is 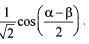
2. The maximum value of the determinant is 1/√2
Q. Which of the above statements is/ are correct?
What is (1000000001)2 - (0.0101)2 equal to?
If A = 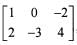 , then the matrix X for which 2X+3A= 0 holds true is
, then the matrix X for which 2X+3A= 0 holds true is
If Z1 and z2 are complex numbers with |z1|= |z2|, then which of the following is/are correct?
1. z1 =z2.
2. Real part of z1 = Real part of z2.
3. Imaginary part of z1 = Imaginary part of z2
Q. Select the correct answer using the code given below:
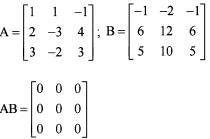
If A = 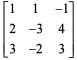 and B =
and B = 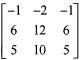 then which of the following is/are correct ?
then which of the following is/are correct ?
1. A and B commute.
2. AB is a null matrix.
Q. Select the correct answer using the code given below:
The number of real roots of the equation x2 - 3 |x| + 2 = 0 is
If the sum of the roots of the equation ax2 + bx + c = 0 is equal to the sum of their squares, then
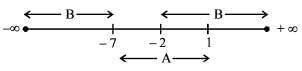
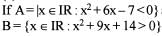 then which of the following is/ are correct?
then which of the following is/ are correct?
1. (A ∩ B) = (-2,1)
2. (A\B) = (-7,-2)
Q. Select the correct answer using the code given below:
A, B, C and D are four sets such th at A ∩ B = C ∩ D = ø Consider the following:
1. A ∪ C and B ∪ D are always disjoint.
2. A ∩ C a n d B ∩ D are always disjoint
Q. Which of the above statements is/are correct ?
If A is an invertible matrix of order n and k is any positive real number, then the value of [det(kA)]-1 det A is
If the roots of the equation
x2 - nx + m = 0
differ by 1, then
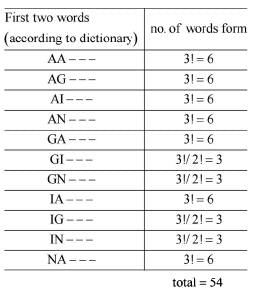
If different words are formed with all the letters of the word 'AGAIN' and are arranged alphabetically among themselves as in a dictionary, the word at the 50th place will be
The number of ways in which a cricket team of 11 players be chosen out of a batch of 15 players so that the captain of the team is always included, is
In the expansion of 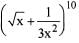 the value of constant term (independent of x) is
the value of constant term (independent of x) is
The value of sin2 5° + sin2 10° + sin2 15° + sin220°+.... + sin2 90° is
Two poles are 10 m and 20 m high. The line joining their tops makes an angle of 15° with the horizontal. The distance between the poles is approximately equal to
If 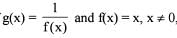 then which one of the following is correct
then which one of the following is correct
Consider the following:
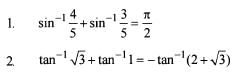
Q. which of the above is/are correct ?
If A is an orthogonal matrix of order 3 and B =  , then which of the following is/are correct?
, then which of the following is/are correct?
1. |AB| = ±47
2. AB = BA
Q. Select the correct answer using the code given below:
If a,b,c are the sides o f a triangle ABC, then 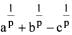 where p> 1, is
where p> 1, is
If a,b,c are real numbers, then the value of the determinant 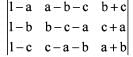 is
is
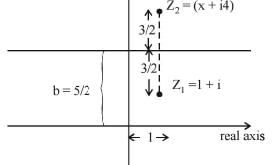
If the point z1 = 1 + i w here i = V-1 is th e reflection of a point z2 = x + iy in the line iz - iz = 5, then the point z2 is
If sin x + sin y = a and cos x + cos y = b, then 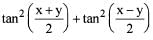 is equal to
is equal to
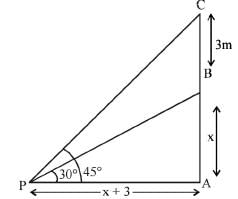
A vertical tower standing on a levelled field is mounted with a vertical flag staff of length 3 m. From a point on the field, the angles of elevation of the bottom and tip of the flag staff are 30° and 45° respectively. Which one of the following gives the best approximation to the height of the tower ?
|
71 docs|22 tests
|
|
71 docs|22 tests
|


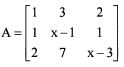
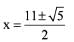

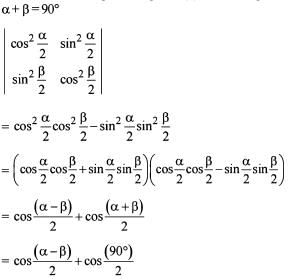


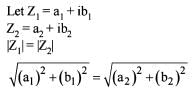
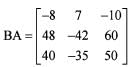
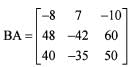

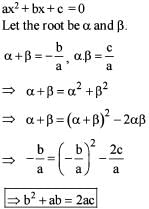
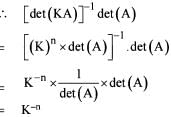
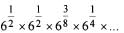 is
is


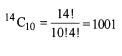

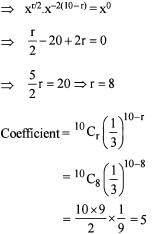
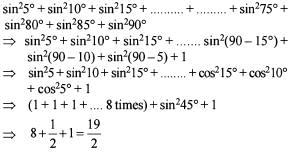
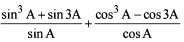 , we get, sin A cos A
, we get, sin A cos A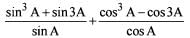
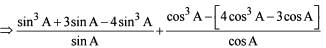
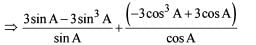
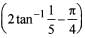 is
is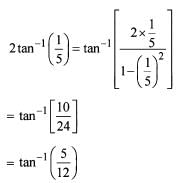
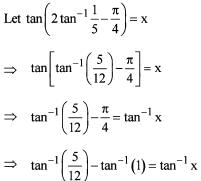
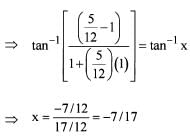
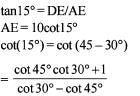
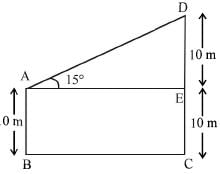
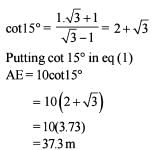
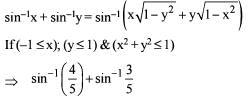
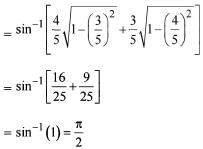
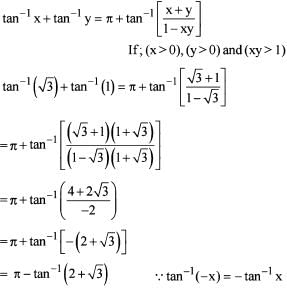 Statement (2) is incorrect.
Statement (2) is incorrect.