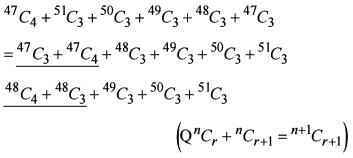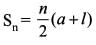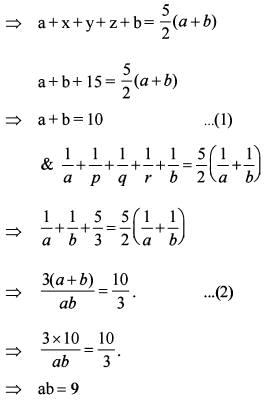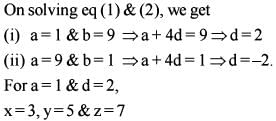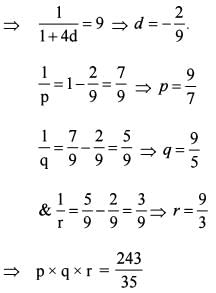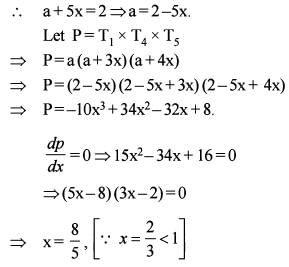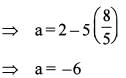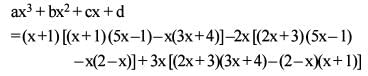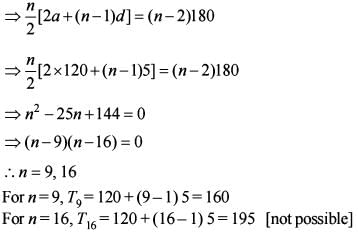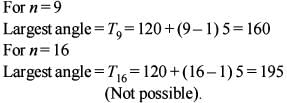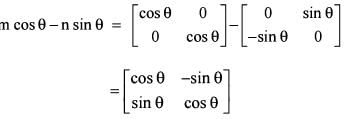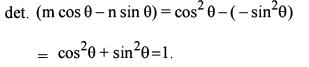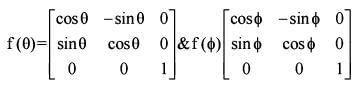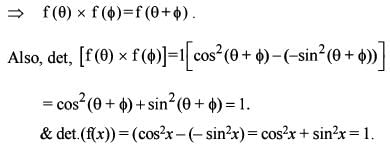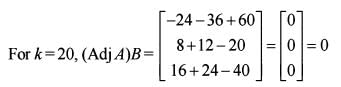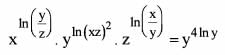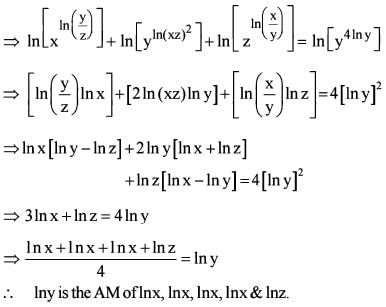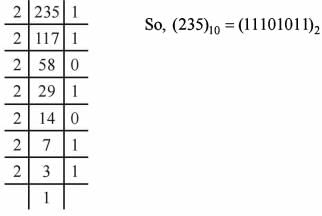NDA II - Mathematics Question Paper 2016 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Past Year Papers - NDA II - Mathematics Question Paper 2016
Let S be a set of all distinct numbers of the form p/q where p , q ∈ { 1 , 2 , 3 , 4 , 5 , 6 } . What is the cardinality of the set S?
If c > 0 and 4a + c < 2b, then ax2- bx + c = 0 has a root in which one of the following intervals?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If A = {x ∈ R : x2 + 6x - 7 < 0} and B = {x ∈ R : x2 + 9x + 14 > 0} , then which o f the following is/are correct?
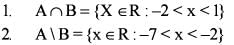
Q. Select the correct answer using the code given below:
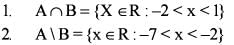
If A is semy square matrix of order 3 and det A= 5, then what is det[(2A)-1] equal to?
What is ω100 + ω200 + ω300 equal to, where ω is the cube root of unity?
 where 2 = x + iy is a complex number, then which one of the following is correct?
where 2 = x + iy is a complex number, then which one of the following is correct?
Out of 15 points in a plane, n points are in the same straight line. 445 triangles can be formed by joining these points. What is the value of n?
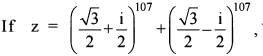 then what is the imaginary part of z equal to?
then what is the imaginary part of z equal to?
If both the roots of the equation x2- 2kx + k2 - 4 = 0 lie between -3 and 5, then which one of the following is correct?
What is the number of distinct solutions of the equation z2 + |z| = 0(where z is a complex number)?
How many geometric progressions is/are possible containing 27,8 and 12 as three of its/their terms?
Let R be a relation from A = {1,2,3,4} to B = {1,3,5} such that R=[( a ,b ) :a<b, where a ∈A and b ∈B]. What is RoR-1 equal to?
A five-digit number divisible by 3 is to be formed using the digits 0,1,2,3 and 4 without repetition of digits. What is the number of ways this can be done?
Consider the following
Let a ,x ,y ,z,b be in AP , where x + y + z = 15. Let a,p, q ,r,b be in HP, where 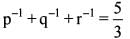
Q. What is the value of ab?
Consider the following
Let a ,x ,y ,z,b be in AP , where x + y + z = 15. Let a,p, q ,r,b be in HP, where 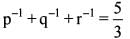
Q. What is the value of xyz?
Consider the following
Let a ,x ,y ,z,b be in AP , where x + y + z = 15. Let a,p, q ,r,b be in HP, where 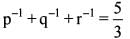
Q. What is the value of pqr?
Consider the following
The sixth term of an AP is 2 and its common difference is greater than 1.
Q. What is the common difference of the AP so that the product of the first, fourth and fifth terms is greatest?
Consider the following
The sixth term of an AP is 2 and its common difference is greater than 1.
Q. What is the first term of the AP so that the product of the first, fourth and fifth terms is greatest?
Consider the following
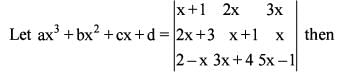
Q. What is the value of c?
Consider the following
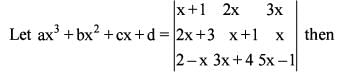
Q. What is the value of a + b + c + d ?
Consider the following
The interior angles of a polygon of n sides are in AP. The smallest angle is 120° and the common difference is 5°.
Q. How many possible values can n have?
Consider the following
The interior angles of a polygon of n sides are in AP. The smallest angle is 120° and the common difference is 5°.
Q. What is the largest interior angle of the polygon?
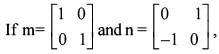 then what is the value of the determinant of m cosθ — n sinθ ?
then what is the value of the determinant of m cosθ — n sinθ ?
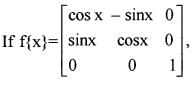 then which of the following are correct ?
then which of the following are correct ?
1. 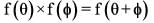
2. The value of the determinant of the matrix 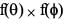 is 1.
is 1.
3. The determinant of f(x) is an even function.
Q. Select the correct answer using the code given below:
Which of the following are correct in respect of the system of equations x + y + z =8, x -y +2z = 6 and 3x -y +5z = k?
1. They have no solution, if k = 15.
2. They have infinitely many solutions, if k = 20.
3. They have unique solution, if k = 25
Q. Select the correct answer using the code given below:
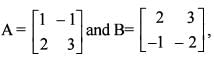 then which of the following is/are correct?
then which of the following is/are correct?
1. AB(A-1 B-1) is a unit matrix.
2. (AB)-1 = A-1 B-1
Q. Select the correct answer using the code given below:
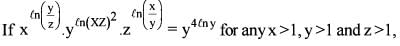
then which one of the following is correct?
If the number 235 in decimal system is converted into binary system, then what is the resulting number ?
|
71 docs|22 tests
|
|
71 docs|22 tests
|



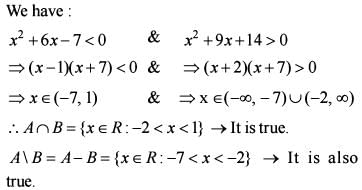
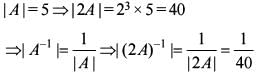
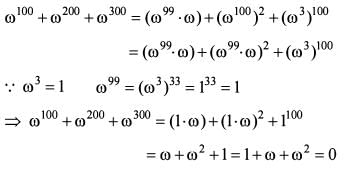

 equal to ?
equal to ? 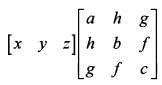
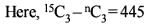
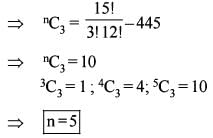
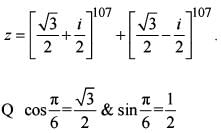
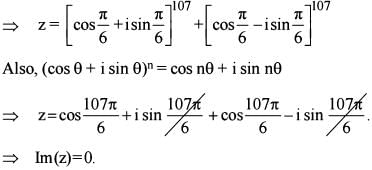
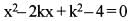
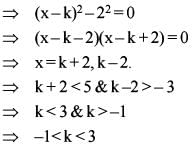
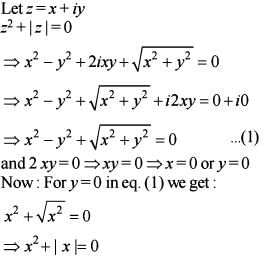
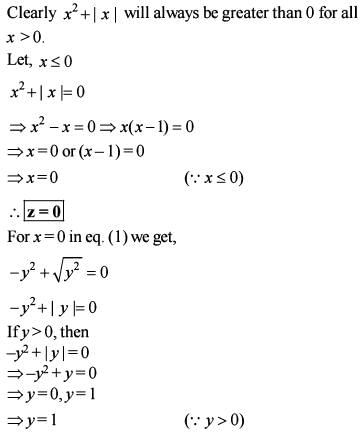

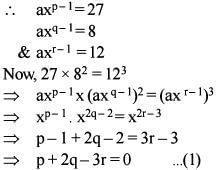
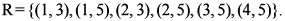
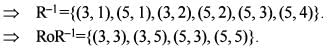
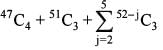 equal to?
equal to?