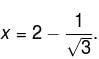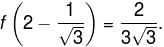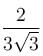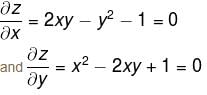Physics Exam > Physics Tests > Topic wise Tests for IIT JAM Physics > Differential Calculus MCQ Level - 1 - Physics MCQ
Differential Calculus MCQ Level - 1 - Physics MCQ
Test Description
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Differential Calculus MCQ Level - 1
Differential Calculus MCQ Level - 1 for Physics 2024 is part of Topic wise Tests for IIT JAM Physics preparation. The Differential Calculus MCQ Level - 1 questions and answers have been
prepared according to the Physics exam syllabus.The Differential Calculus MCQ Level - 1 MCQs are made for Physics 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Differential Calculus MCQ Level - 1 below.
Solutions of Differential Calculus MCQ Level - 1 questions in English are available as part of our Topic wise Tests for IIT JAM Physics for Physics & Differential Calculus MCQ Level - 1 solutions in
Hindi for Topic wise Tests for IIT JAM Physics course. Download more important topics, notes, lectures and mock
test series for Physics Exam by signing up for free. Attempt Differential Calculus MCQ Level - 1 | 10 questions in 30 minutes | Mock test for Physics preparation | Free important questions MCQ to study Topic wise Tests for IIT JAM Physics for Physics Exam | Download free PDF with solutions
Differential Calculus MCQ Level - 1 - Question 1
The functIon u(x, y) = x2 + xy + 3x + 2y + 5 has a point of :
Detailed Solution for Differential Calculus MCQ Level - 1 - Question 1
Detailed Solution for Differential Calculus MCQ Level - 1 - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Differential Calculus MCQ Level - 1 - Question 3
The points on z2 = xy + 1 nearest to the origin are :
Detailed Solution for Differential Calculus MCQ Level - 1 - Question 3
Differential Calculus MCQ Level - 1 - Question 4
The values of x1 and x2 with x1 < x2 such that 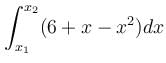 has the largest value are :
has the largest value are :
Detailed Solution for Differential Calculus MCQ Level - 1 - Question 4
Differential Calculus MCQ Level - 1 - Question 5
The sum of two number is k. The minima value of the sum of their squares is :
Detailed Solution for Differential Calculus MCQ Level - 1 - Question 5
Detailed Solution for Differential Calculus MCQ Level - 1 - Question 6
Differential Calculus MCQ Level - 1 - Question 7
For the function x2 + y2, (0, 0) is a point of :
Detailed Solution for Differential Calculus MCQ Level - 1 - Question 7
Differential Calculus MCQ Level - 1 - Question 8
If dy/dx = (x - a)2n (x - b)2p + 1, where n and p are positive integers, then at x = a, x = b, f(x) has respectively :
Detailed Solution for Differential Calculus MCQ Level - 1 - Question 8
Differential Calculus MCQ Level - 1 - Question 9
The maximum value of (x – 1)(x – 2)(x – 3) is :
Detailed Solution for Differential Calculus MCQ Level - 1 - Question 9
Differential Calculus MCQ Level - 1 - Question 10
The saddle point of the function z = x2y – y2x – x + y is :
Detailed Solution for Differential Calculus MCQ Level - 1 - Question 10
Information about Differential Calculus MCQ Level - 1 Page
In this test you can find the Exam questions for Differential Calculus MCQ Level - 1 solved & explained in the simplest way possible.
Besides giving Questions and answers for Differential Calculus MCQ Level - 1, EduRev gives you an ample number of Online tests for practice


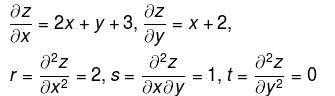
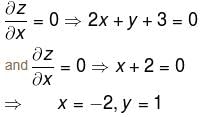
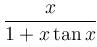 is maximum at x= :
is maximum at x= :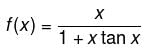
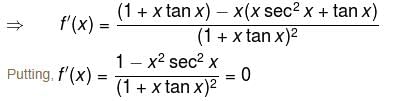

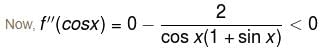
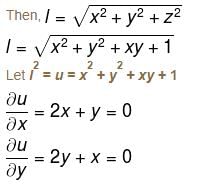
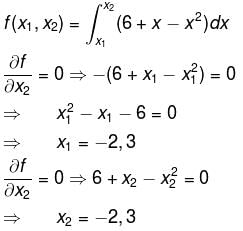
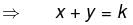
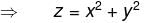
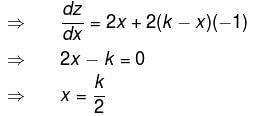
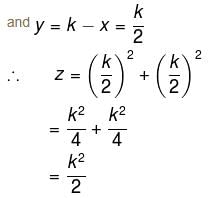
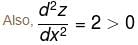
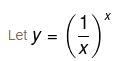
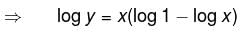
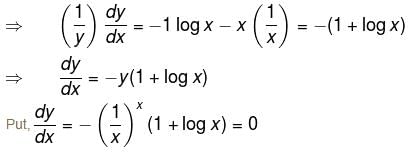
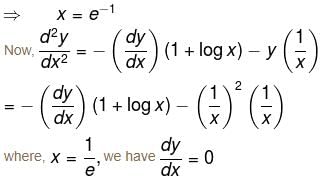
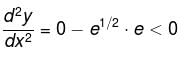
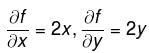
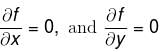
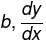 is negative as 2p + 1 is odd.
is negative as 2p + 1 is odd.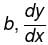 is positive. Thus, y is minimum at x = b.
is positive. Thus, y is minimum at x = b.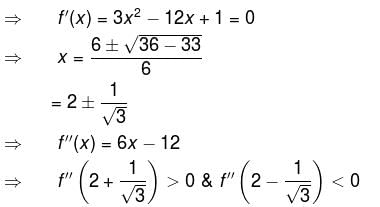
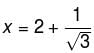 and f(x) has maxima at
and f(x) has maxima at