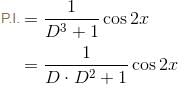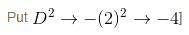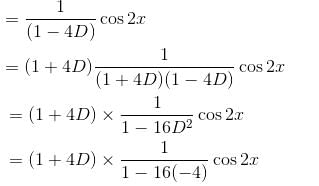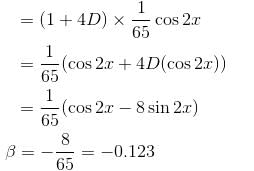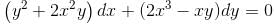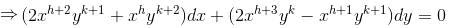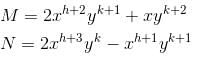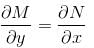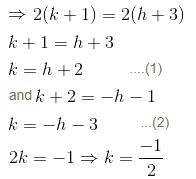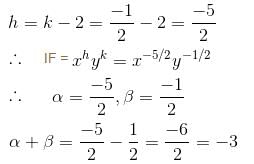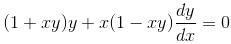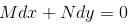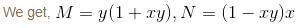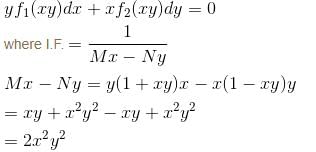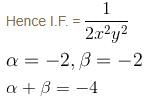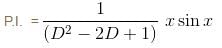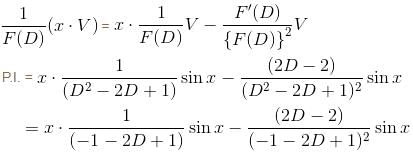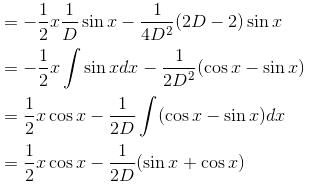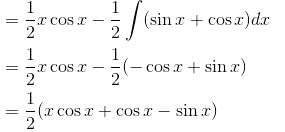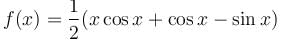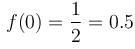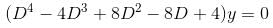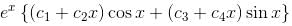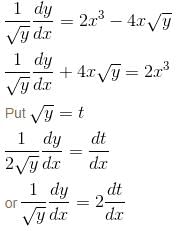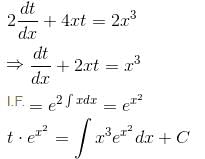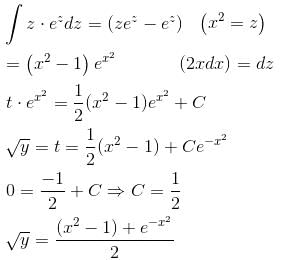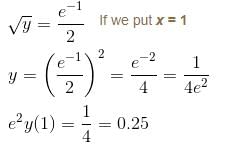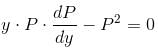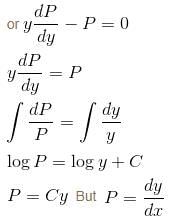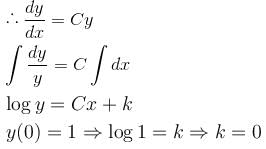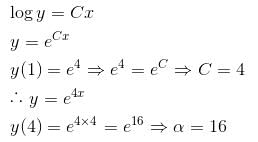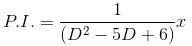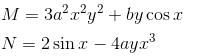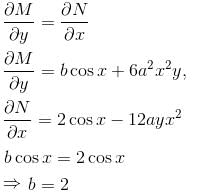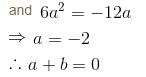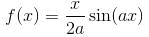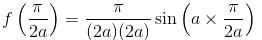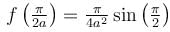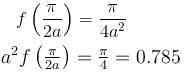Differential Equation NAT Level - 1 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Differential Equation NAT Level - 1
If the Particular Integral (P.I.) of the differential equation (D3 + 1)y = cos2x. is given by y = 1/65 (cos 2x - β sin 2x). Find the value of β
I.F of differential equation (y2 + 2x2y)dx + (2x3 – xy)dy = 0 is of the form xαyβ. Then find value of α + β
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The IF for the Differential Equation (1 + xy)y + x (1 - xy)dy/dx = 0 is xαyβ. Then find the value of the α + β.
Find the value of f(0) where f(x) is the Particular Integral (P.I.) of the Differential equation (D2 –2D + 1)y = x sin x.
Solve 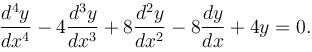 In the solution find the value of constant which is in multiplication with cos x only given y(0) = 0.
In the solution find the value of constant which is in multiplication with cos x only given y(0) = 0.
Let y be a function of x satisfying dy/dx = 2x3 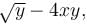 y(0) = 0, then find the value of e2y(1).
y(0) = 0, then find the value of e2y(1).
Given a differential equation 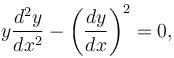 y(0) = 1, y(1) = e4, then y(4) = eα . Find the value of α.
y(0) = 1, y(1) = e4, then y(4) = eα . Find the value of α.
The Particular Integral (PI) of the differential equation (D2 – 5D + 6)y = x is given as y = mx + c. Find the value of c.
If the differential equation (3a2y2x2 + bycosx)dx + (2sinx – 4ayx3)dy = 0 is exact then what is the value of 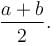 a, b ≠ 0.
a, b ≠ 0.
If the Particular Integral (PI) of the Differential equation (D2 + a2)y = cos ax is given by f(x). Then find the value of a2f (π/2a).