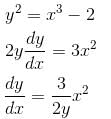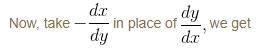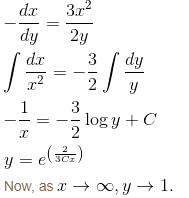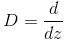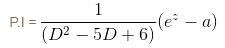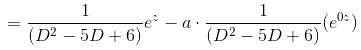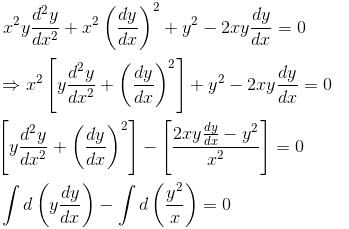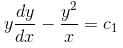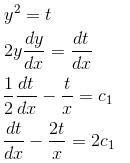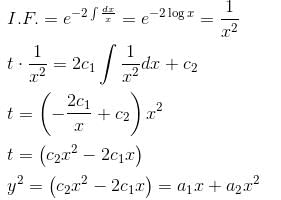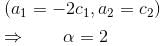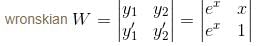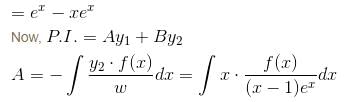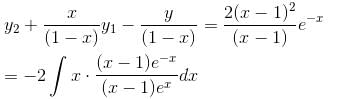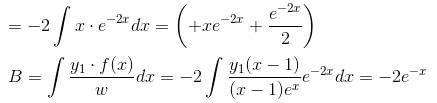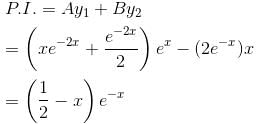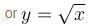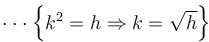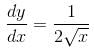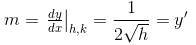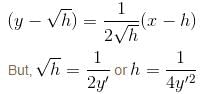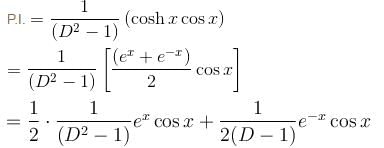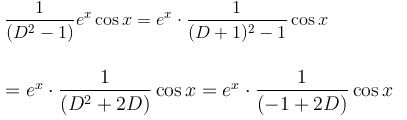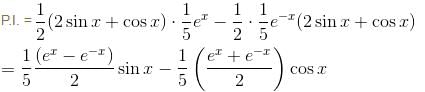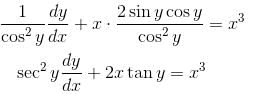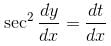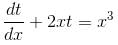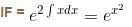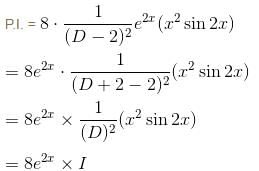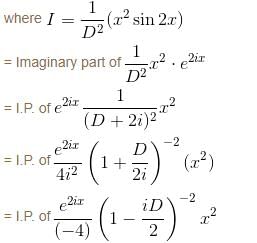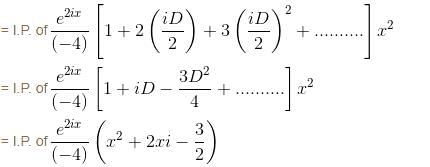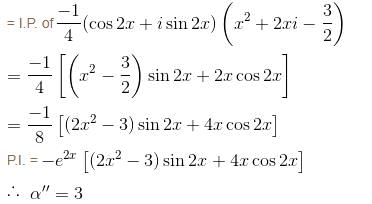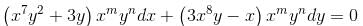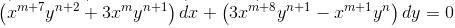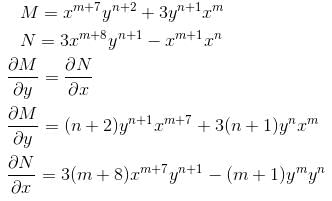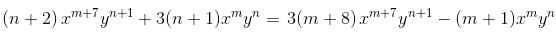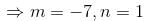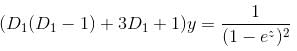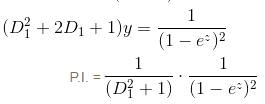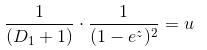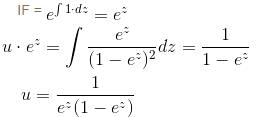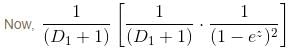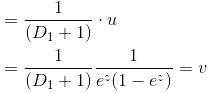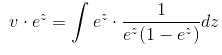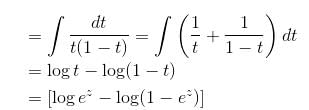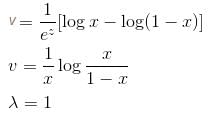Differential Equation NAT Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Differential Equation NAT Level - 2
Find the orthogonal trajectory of the family of curves, y2 = x3 – 2 so, find the value of y as x → ∞.
If the P.I. of the Differential Equation  is of the value form
is of the value form 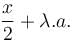 Find the value of λ.
Find the value of λ.
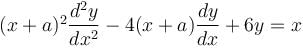 is of the value form
is of the value form 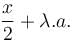 Find the value of λ.
Find the value of λ.| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the solution of 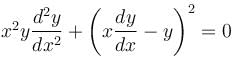 is of the y2 = a1x + a2xα. Find the value of α.
is of the y2 = a1x + a2xα. Find the value of α.
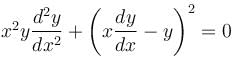 is of the y2 = a1x + a2xα. Find the value of α.
is of the y2 = a1x + a2xα. Find the value of α.If ex and x are solutions of Homogeneous equations (1 – x)y2 + xy1 – y = 2(x – 1)2e–x then the general solution y is of the form y = c1x + c2ex + α - xe-x. Find the value of α.
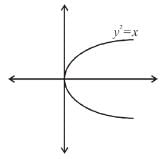
Find the order of differential equation of all tangents to parabola y2 = x
If the P.I. of the differential equation (D2 – 1)y = coshxcosx is of the form α.(2 sin hx sin x - cosx).
An integrating factor of the equation dy/dx + x sin 2y = x3 cos2 y is f(x). Find the value of f(0).
If the PI of differential equation (D2 - 4D + 4) y = 8x2e2x sin 2x is of the form eαx [(α'x2 + α") sin βx + β' x cos βx] then find the value of α".
If the integrating factor of the differential equation (x7y2 + 3y)dx + (3x8t - x)dy = 0 is of the form xmyn then sum of values of m and n is :
If the P.I. of Differential Equation (x2D2 + 3xD + 1) y = 1/(1 - x)2 is of form  then, find value of λ.
then, find value of λ.